Simple Nano Circuit 开发日记(32)
这个软件截至昨天,应该当是一个小的阶段完成——可以初步实现直流电源、电阻构成的电路中各个网络节点的电压求解。起初觉得神秘,做过一遍发现背后的数学原理十分简单,只需要根据电路创建线性方程组,然后求解即可。 下一阶段知识难度估计会大幅度提升,为了迎接下一阶段的挑战,我想还是应该先把当前的工作重新整理、封装,确保现在的代码稳固。因而今天开始做代码的收敛工作。 首先是将之前遗留的若干问题要逐一解决掉,其中既有bug,也有功能的缺失。今天主要完成了以下工作: 1、线性方程组构建中存在一个缺陷,引发了在开路时的电压计算错误,这是方程组中的节点方程构建时,没有考虑到悬空引脚导致的; 2、对代码中若干冗余的方法进行清理; 3、对代码中若干传值的地方进行调整,改成传递引用; 除此之外,还有一些功能上的缺失也要在接下来几天逐一完成: 1、对已放置的IC进行删除、移动等操作; 2、对已放置的IC进行选取,通过弹窗对它们的属性值进行调整。 如上工作全部完成之后,便可以将“交流电源”引入进来,从而产生“时间”的概念,为后续增加非线性元件打下初步基础。 Update 2024.12.28 Day: 33 SLOC: 5012 下午到了家乐福,晚上吃的牛肉面。吃牛肉面之前的一段时间: 1、完成了弹窗修改 电阻 和 直流电源电压 的功能; 2、完成了这个弹窗机制的通用化,也就是说所有的IC,都从基类定义是否可以弹窗,如果可以弹窗,就在IC自己的类内实现弹窗风格和窗口内容设置; 然后下楼吃牛肉面,去的路上想明白了线路中的电流是怎么计算的,没有偷懒的途径,必须对线段进行分割,才能实现电流的分段计算。所以吃完牛肉面回来,开始着手进行线路分割操作。 分割线路的整体思想很简单:落PIN时,判断落PIN是否压中了线段,如果压中线段则对已压中的线段按PIN进行切割;画线时,则是判断线段是否穿越了PINs,如果穿越了PINs,就一次找到每一个PIN同样以PIN为分割点、对线段进行分割。 完成这个功能之后,又进行了一下“清理电路中冗余线段”的功能实现。 1、如果某线段两端有任意段悬空,则将这条线段标记为冗余线段,完成一次检测之后,将所有检测到的冗余线段删除掉(注意此时还要删除连带的可能的冗余网络节点、冗余网络节点存储器等)。…
Simple Nano Circuit 开发日记(30)
Day: 30, SLOC: 4614。 最近几天小仿真软件写的有些怠慢,代码膨胀比较厉害。好在终于将主要想法实现了出来,接下来将用2-3天填补遗留的若干缺陷、再花上一周左右做一做代码收敛和文档补全。之后便可以继续下一阶段的开发了。接下来将完成交流电源,再把电感和电容加进来。功能开发的脉络虽然清晰,但实际上这对我而言还是非常有挑战的:当电路只有电阻时,仿真求解只需用到线性代数,可一旦引入了电容和电感,将会用到微分的知识,期望用到的知识点不会太多、太难。 Day: 31, SLOC: 4635。 今天代码与昨天比起来,增加的并不多,但实际上也是做了一些工作的,因为主要是对原有代码进行修缮,所以单纯代码行数上看不出来什么。但借助 git diff 可以看出来,今天也是进行了200多行代码的调整。 主要是解决了此前遗留的奇异矩阵求解问题。 当矩阵是奇异矩阵时,程序会尝试去求解一个元,完成这一个元的求解之后,再次判定矩阵是否是奇异矩阵:如果依然是,则放弃此次求解;如果已经不再是奇异矩阵,就进行求解。 上面这个是之前的思路,然而上面这个思路其实是存在问题的,正确的做法是:如果奇异矩阵在完成了一次解奇异之后,依然是奇异矩阵,可以再次尝试解奇异:如此反复解无可解才认为矩阵无解。若是经过了多次解奇异之后满秩了,那么就可以求解了。 从以上错误的做法到正确的做法,就是今天主要完成的工作。 除此之外还做了一些其他的调整:为 Pin 引脚增加了一些属性,这样在进行相关的运算时就不用再通过引脚找到它的 IC 再去做 IC 判定,引脚在创建时就已经将 IC 信息记录下来,用的时候直接询问就可以了。 同时,引脚不仅记录着…
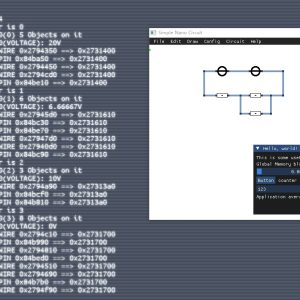
Simple Nano Circuit 开发日记(29)
Day: 24, SLOC: 3500。与其使用完善的、成熟的、现成的仿真软件,不如自己半学半写的实现一个,这样一来可以学习C++编程语言;二来可以把自己荒废了多年的数学重新捡起来看一看、读一读;三来能对电子元件的特性有更全面的了解。这个小软件没有甲方,做起来也就更有乐趣、更从容一些,我考虑就是尽量不引入太多第三方依赖,让它尽可能的小一些。 Day: 29, SLOC: 4263。完成了对 MathMatrixClass 的独立封装,因为增加了对矩阵的分块、奇异性判断,所以可以得到整个系统中的电路彼此不连通的各个局部电路。又通过奇异矩阵判定出电路无解,通过解奇异尝试,若能解除奇异便可再次尝试求解。若无法解除奇异、或者无论如何都无法求解,也不会终止程序,就对那块子矩阵不处理就好了,能求解的部分求解出来。 这样做的好处是更接近物理现实,也许对于成熟的仿真软件,它们还有更复杂的考量,但是以我现在的认知而言,我觉得当前的做法更接近物理现实一些。 因为加入了解奇异尝试,所以已经可以正确的推导出网络节点的正确电压,我并没有在没有“地”的时候默认电源负极为地,而是通过解奇异之后,依然有程序去尝试矩阵求解,这样的出来各个节点电压,看上去效果也是正确的。

SDL2中纹理旋转的小困惑
这几天使用SDL2练手一个小应用,其中有个需求是期望对纹理进行旋转,结果发现:不旋转时显示正常,一旦旋转之后输出的图形就会发生很严重的扭曲。 之所以产生这个现象,是因为我创建的这个纹理并不是正方形,而是一个长和宽不相同的矩形(长方形)。现在虽然找到了原因,也通过临时创建了一个正方形来暂且解决了问题,但心中总难免觉得“膈应”。还是期望能够有更正确的解决方案,以正确实现这个需求。 在写完上面的“备忘”之后,又经过了一天的时间,现在已经对长方形的旋转进行了两次改良,感觉应该是已经基本正确、完美的实现了对长方形纹理的旋转。以下是这篇文章的思想脉络: 以下是详细的记录: 一、无法正确完成长方形纹理旋转的现象 在SDL2中,创建了一个32*16的纹理,暂且称这个纹理为“一杆长枪”吧。这个“一杆长枪”的纹理本来是水平渲染到屏幕上的,看上去就是一把图像准确的“长枪”。 我期望是使用键盘的M按键控制纹理旋转,我的旋转策略非常简单,每次按下M按键,只会顺时针产生一次90度的旋转,因而长枪或者水平出现在屏幕上、或者就是竖直的出现在屏幕上。这个需求并不复杂,也没有必要考虑其他刁钻的角度,感觉应该很容易实现。 然而当我完成了代码的撰写之后,长枪水平出现在屏幕上时,的确是正确的。可一旦旋转了90度之后,长枪并没有如预期的竖直的出现在屏幕上,而是竖直、却被压扁了的出现在了屏幕上——渲染结果是竖直的“手枪”出现在了屏幕上。 在反复的胡乱修改代码过程中,还有一些时候会出现如下各种更加离谱的情况: 当然以上更加离谱的情形实际上是我的代码完全不正确导致的。实际上代码如果正确,只可能出现一种情况:水平时是长枪、竖直时是短枪。 二、导致问题出现的原因 经过将近一天的排查,最终才搞清楚原因:SDL_RenderCopyEx()方法虽然的确可以完成旋转,但是它在不指定原纹理、新纹理的尺寸时,是会自动进行一定的缩放的——它会依渲染目标区域先对图像进行缩放、然后才进行旋转操作。 网上之所以没有这个问题的讨论,是因为大家或者没有我这样的需求、或者就是有我这种需求但实现的都是正确的,没有人入坑、自然也就不会有人讨论。 我的需求有一个“坑”:纹理并不是直接绘制在“屏幕渲染区域上”,而是纹理渲染在“与纹理相同的渲染区域上”。这个细微的差异引起了我所遇到的问题。 如果纹理是被渲染在屏幕上,屏幕一般都是在640×480以上,显然的:对于一杆32×16的长方形“长枪”,无论怎样旋转,都会在640×480的内部展现出来,不会发生扭曲。 然而如果期望的是:将32×16的长枪,渲染到16×32的渲染区中,就会出现各种各样的问题了: 起初:是将32×16的长枪,渲染到32×16的渲染区中,这个时候长枪不用进行旋转,显示正常:水平的长枪; 然后按下了键盘上的M按键,程序开始对长枪进行旋转处理:我的程序逻辑是:创建一个新的16×32的渲染区域,然后将32×16的长枪通过SDL_RenderCopyEx()复制进入16×32的渲染区域、并同时进行90度的旋转。此时,SDL_RenderCopyEx()内部的操作很可能是:先将32×16的纹理资源贴入16×32的渲染区域中,因为没有指定缩放,所以它自行进行缩放,将长枪从32×16缩放成了16×8,然后再进行旋转,最终得到了一个8×16的竖直图像并呈现在16×32的渲染区域中。 上述描述不够直观、但我也不想额外画图说明这个事情了,总之大概意思就是这样——旋转之后的图案总是会出现各种各样的扭曲情形。 三、粗糙的、简易的解决方案 知道了原因,解决起来就比较容易了,但实际上也并不是一帆风顺的。我起初是退而求其次的放弃了32×16这样的“长方形”,而是将软件中用到的所有图形,都做成了32×32的图形,这样无论怎样旋转(只要不出现30度、45度等非直角角度),一定可以正常显示。 然而这种退而求其次的方法并不可行——毕竟软件后面还有很多功能要基于正确的资源尺寸进行进一步的开发。 所以第二次调整改成了更复杂的一个方案:长枪还是32×16的纹理资源,但是每次想进行重新旋转的时候,渲染显示区域都先创建一个32×32的显示区、然后完成旋转之后放在这个32×32的显示区域中。再重新创建一个正确的16×32的显示区,将32×32显示区中的竖直长枪复制出来、写入到16×32的显示区中…… 这虽然是可行的,但是浪费内存、CPU资源不说,更令程序变得十分复杂。要额外的记录很多临时数据、还要计算数值长枪在32×32区域中的正确位置才能准确裁切出来。 以上两个方案都是“自然而然”想到的方案,虽然“思路清晰”、但是“实现复杂”并且总是感觉存在着诸多的隐患。 四、更正确、完美的解决方案 今天我才想明白:其实没有必要让SDL2去进行纹理的旋转,SDL2的SDL_RenderCopyEx()进行纹理旋转有它巨大的优势——对于各种角度的旋转都可以轻松胜任。然而我也用不到这些角度呀,我只需要进行90度、180度、270度的旋转,这几个最基本的旋转就是最基本的矩阵90度旋转。…

控制台中VIM编辑中文时字符鬼影问题的解决
这个问题困扰我好久了,也不记得是什么时候开始的,也许是自从开始使用PowerShell时就出现了这个问题?控制台下使用VIM进行中文编辑,如果当前行有中文,那么这一行的内容编辑、选中,总会在行尾甩出一些鬼影字符。 因为近几年程序写得少、偶尔遇到这个问题就会换用其他编辑器临时救急,所以也就没放在心上。今天实在忍受不了,折腾了一个晚上终于找到了原因并解决了。 在vimrc配置中加入一行 set termguicolors 即可解决: 虽然说加入这行配置之后会导致vim的颜色配置与默认配置有了一些差异,但终归还是“彩色渲染”的代码,修改前后都是“赏心悦目”的状态,因而对于使用也没有什么影响。 这行代码的作用是让vim改用真彩色进行文字渲染,否则vim默认使用的是256色对文本进行渲染。而默认使用256色彩模式时,在显示复杂的 Unicode 字符(如中文字符)时,就有可能导致显示问题——无法正确计算出字符的宽度、从而引起鬼影问题。 上面的解释听起来很牵强,色彩管理和字符宽度能有什么关联呢……但毕竟它真的能解决问题,因而也就不再纠结其中的因果联系了。 奇怪的是用了很多年vim,以前从来没有察觉这个问题,似乎是最近1、2年才出现的问题。毕竟最近很少写代码,偶尔写一写、遇到稀奇古怪的编辑器问题也都是尽量避开,有的时候犯懒甚至就用notepad临时改动几行,所以也没有去深究过。感觉可能是: 1、或者就是自从windows弃用了控制台、启用了powershell之后出现的这个问题; 2、又或者是这个问题一直存在,只不过以前我在windows下一直使用的是neovim所以没有这个问题吧; 不确定,总之,经过上述调整,现在vim又可以正常的对中文内容进行编辑操作了。
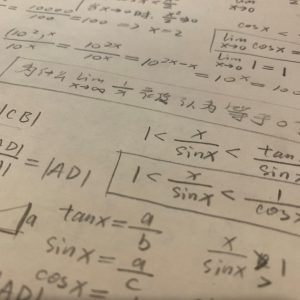
使用ε-M极限证明问题一则
为什么? 直观上的感觉是,x趋于无限大,它的导数便趋于0,于是也便趋于0,最终的极限结果就是0了。这似乎很简单。但如果基于数学分析的角度而言,这每一步的理所当然,都需要经过证明,所以对于数学分析而言,这个简单的极限的推导过程,并不轻松,而是要啰里啰唆的说上一大堆,才敢给出结论来的。 它大体上分为两步:1、首先证明;2、然后利用连续函数的复合法则,完成复合函数求极限。以下是每一步的细节: 一、首先使用语言证明: 《普》中并未給出的證明、甚至都沒有提到這一事實,它似乎是默認讀者知道且相信這一極限的結果。這個簡單的極限從直觀上也確實一目瞭然,但是在更嚴謹的數學教材中,其實是會通過語言對它進行證明的。語言和語言相似,都是極限論證語言。使用语言完成证明的过程如下: 1、首先观察原始的题目,并且将原始题目调整一下写法:; 2、这个新的写法不再使用“等号”,从而表达式的意思变成了:当自变量x趋于无限大时,结果(因变量)将趋于0。调整成这样的表达之后,假设这个结论是成立的,那么它将意味着计算的结果与它所趋近于的数值0之间,是存在着一个距离的,而且这个距离可以表达出来,将这个距离表达为:; 3、此时 的含义就是“距离”,并且是 与 之间的距离。我们要证明的是,这个距离 可以任意的小、随意的小,想要多小就多小。换言之,假设 的确可以任意的小能够实现,意味着 与 可以无限接近,便可以将 视为 了; 4、现在直接大胆的提出:当任意指定时,自变量 时,的结果就比还要小。能否找到这个大胆的想法中的M呢?显然是可以的,通过不等式简单的变换,就能确定,也就是说自变量 时的所有x取值,都可以满足 的结果比还要小; 5、至此就可以得出结论:无论怎样小的 指定,都有 M 范围选择点可明确出来。因而可以实现,并且认为。此时的表达式便是:。(这里似乎还缺少对下标 的展开推导)。 二、连续函数的极限连续性:…

再谈昨天的“沃利斯积分“
昨天写的《沃利斯曾经解决过的几道积分问题》还存在一个令我感到“困惑”的问题,今天解决了,很开心。 昨天的文章中提到的积分:,通过换元法可以得到它的三角函数形式、也就是沃利斯积分形式:。而这两个等价的积分式又可以被统称为B积分,进而推导成Gamma计算式,完成求解。 这是昨天的文章中谈到的内容,结论无疑。 但是我的困惑在于:当我对上面诸多计算式,分别通过笔算、SageMath计算、计算器计算对比验证的时候,却发现我使用的计算器无法得到正确的结果,现象如下: 积分 积分式 Gamma结果 SageMath结果 fx-991CN结果 多项式积分 正确 正确 正确 沃利斯积分 正确 正确 1.569…… 问题现象表 可以看出我使用计算器得到的结果并不是正确的,原因在于在这个计算器的设置中有结果表达形式的设置,之前使用的是以数值作为结果表达形式,应该调整成使用弧度作为结果表达形式,通过这个设置的改变,才能得到正确的结果。 之所以要如此繁复的、不厌其烦的做这个验证,主要是心里没底,担心自己理解的不对。现在所有的辅助自动计算结果都与理论吻合、手算结果一致,我就可以放心大胆地说,这个知识点,我算是基本掌握了。 对于计算器,今天在查找它的设置时,额外了解到:计算器在进行积分计算时,使用了很多估算方法,例如辛普森法、梯形法、或者高斯-勒让德积分等。通过这些方法,计算器在给定积分区间内选取若干采样点,以近似计算积分值。 这些数值积分算法对我而言还很陌生、又觉得好奇有趣,只无奈精力实在有限,无法深入学习。

沃利斯曾经解决过的几道积分问题
在斯科特撰写的《数学史》一书中,P148页有一段简单的描述:沃里斯曾仿照卡佛来利的方法解决了纵坐标由的求积问题。 书上给出了如下若干积分及计算结果: 1、 2、 3、 4、 上面这4道题看起来还都是比较容易的,即便是第4题,只是计算量略微繁琐,但只要通过分部积分的方法,依然可以轻松得到答案。下面仅以第3题为例动笔跟着练习一下: 题目:计算 首先将多项式展开,然后利用分部积分法,对每一个简单积分进行求解,最终求和: 之所以使用第3题练笔,原因是后面的第4题如果如上方法推导的话,展开项更多,繁琐、浪费笔墨、且容易出错。但假设问题更复杂一点,例如想计算,恐怕就不再是“有一点繁琐”,而是会非常繁琐、几乎无法完成的事情了。 所以上面一系列相似的问题,还是应该再找一找更为通用、便捷的工具进行计算。自然而然的想到了利用换元法进行计算。以上面第4题为例尝试一下改用换元法完成计算吧: 考虑到积分范围是从0到1,计算式中又明显能够感受到毕达哥拉斯的味道,因而尝试对进行换元:。 换元准备1:重新调整积分上下限: 换元准备2:计算式换元: 换元准备3:微分项还原: 通过以上准备,最终完成换元: 至此问题得到了简化,能够看出最终的换元结果成为了B函数形态,将B函数原形写出来,目的是计算出B函数参数式: 即通过:, 可得到: 指明参数的B函数是: 使用转换: 最终得到Gamma函数: 其中,, 将以上三项计算结果带回Gamma计算式,得到最终结果 附:沃里斯简介 约翰·沃里斯(John Wallis,1616-1703)是17世纪英国著名的数学家、逻辑学家,也是剑桥大学三一学院的毕业生,后来成为牛津大学的萨维尔几何学教授。沃里斯在数学、物理学、密码学等多个领域做出了重要贡献,对微积分的早期发展也产生了深远影响。
两道极限计算的简单题目
两道题目如下: 1、计算: 2、求证: 一、计算: 解法1:极限定理法 当x趋于无穷时:分子是个正弦反复跳跃、极限不存在;分母x趋于无穷、极限也不存在。因而分子和分母都没有明确的极限值的情况下,无法用商的极限运算法则进行计算。 考虑使用乘积的极限运算法则进行计算:。 分解出来的两个因式的结果分别是有界函数和无穷小,他们的乘积等于0。 解法2:三明治法 因为,所以 左边有: 右边有: 不等式两端在x趋于无穷时,同时趋于0,所以中间的极限 二、证明: 这个证明比较难、甚至是非常难。虽然在《高等数学》和《普林斯顿微积分读本》的开始、最基础的章节中就有这个重要极限的介绍、以及证明。但实际上这两本书都故意忽略了一个基础极限:。 在《高等数学》§1.7中,这里几乎是“一笔带过”假装“显而易见”糊弄过去了;在《普林斯顿》§7.1.5中则是给出了上面的结论而也语焉不详的糊弄过去的。 两本书用的证明方法相同、也都忽略了上面提到的基础,我也先忽略、假装是个事实,完成证明:基本思想依然是利用三明治定理,设法找到两边的函数,通过两边的极限,夹近出的结果。 构建如上图形,其中圆为单位圆、半径,可以看出:,这个不等式的左中右分别为: 左侧: 中间: 右侧: 带入不等式,得到:, 将这个不等式各个部分除以并颠倒分子和分母、简单整理之后得到: 左侧:,注意这里是“假装显而易见先糊弄过去”; 右侧:, 通过三明治定理,即可夹近出中间的极限:。 注意上面的三明治极限都是取的,这是因为原式中的分母不能取0点,因而要分别求它的左极限和右极限,上面只是在计算右极限。相应的进行符号斟酌、调整,可以再求出左极限:。…

爱因斯坦的日全食实验
阿尔伯特·爱因斯坦曾在他的相对论中提出了一个著名的日全食实验,后来几经波折,最终被英国天文工作者和科学家们实施、最终证实了爱因斯坦关于光线会受重力场影响的观点及理论的正确性,这一理论和实验,标志着爱因斯坦相对论的正确性,从而轰动世界。 2019年5月16日,葡萄牙发行了一套关于爱因斯坦日全食实验的纪念邮票,包含邮票、首日封、小型张等多款邮品,官方介绍如下: 发行官网:https://www.ctt.pt/邮票技术手册:邮票官方介绍手册 这套纪念品中的邮票由2张票面构成,如果单看票面,只能知道它是纪念爱因斯坦提出的日全食实验,并不能对实验的具体原理详尽了解。在随邮票一同发行的产品手册中,则有着更多的信息介绍,可以清楚的看出实验的设计想法:通过在日全食时观察通过太阳周围临近恒星的位置,观察到光在重力场下会发生偏转、扭曲的事实。 爱因斯坦最初大约是在1905年时提出的狭义相对论,其中提到光线会被重力影响。但是最初的论文中并没有这个理论的设计实验,之后1907年时他对之前的论文进行补充、并在4年之后的1911年形成了一篇关于光线受重力影响的“补充论文”,其中给出了具体的理论公式和实验方案。在其理论计算下得出了光线可受太阳引力影响发生偏移的角度。这篇论文的原文和英文版在网络上可以找到。 上面是英文翻译版,下面是这篇论文的原稿: 然而在1911年提出这个实验时,并没有合适的日食事件可供实施这一实验。爱因斯坦呼吁当时的天文学家可以充分利用这段“等待期”进行筹备,他对这个观测实验十分期待并且投入了大量的精力以极力促成此事。 当时柏林大学天文台有一位年轻的天文学家埃尔文·弗伦德里希(Erwin Freundlich),读到了上面提及的论文和实验方案,他对此十分感兴趣,便与爱因斯坦联系并一同商讨进行此次天文观测。虽然如此,但限于爱因斯坦当时的学术权威和声望并不高,他的构想在当时并未获得更多人的支持,尤其是资金方面的支持。因而爱因斯坦甚至提出可以自己承担一部分费用、他给了弗伦德里希2000马克的资金用于初期准备。 就在前期准备得差不多、距离1914年8月的一次日全食不到20天时,第一次世界大战爆发了(1914年7月28日),德国裔的天文学家弗伦德里希在克里米亚被发现,俄国人认为随身携带着大量“摄影器材”的“天文学家”十分可疑,所以将他拘捕。从而失去了那一年日全食观测的机会。 想再一次盼到日全食,对于人类而言只能期待、别无他法。时间慢慢到达了1919年,是年5月29日将再一次发生日全食现象,好在那时战争已经结束(一战结束于1918年11月11日)。当时英国剑桥天文台的台长、天文学家阿瑟·斯坦利·爱丁顿(Arthur Eddington)决定完成爱因斯坦关于光线的实验——对当年的日全食进行观测和拍照。 整个实验都是由英国天文学家们共同策划、由英国相关部门出资支持的。这在当年很罕见,毕竟爱因斯坦当时身在德国、而英德两国在1919年时的关系并不友好。这一点上看来,科学家们似乎并不关心政治、也不在乎国与国之间的矛盾,他们向往和关注的只有科学和真理。 经过紧罗密补,1919年3月初,爱丁顿等人从利物浦出发,分成两支实验团队分别前往巴西北部的亚马逊丛林和普林西比岛,这两处都有着最佳的日全食观测地点。 之后的事情妇孺皆知、也是这套邮票上体现出来的了:1919年5月29日,由爱丁顿科考队在普林西比岛获得的照片最终被选用为实验结论样本,并通过后期的图像分析和计算,验证了爱因斯坦的光线理论。从而为相对论的底层补充上了重要的、无可动摇的实验依据。