设 \(0 < x_1 < 3\),若定义 \(x_{n+1} = \sqrt{x_n(3-x_n)}\),其中 \(n=1,2,\cdots \)。此时的数列 \(\{x_n\}\),是个递增数列还是递减数列?或者说它并不是单调的?
我看书上说这个数列是一个递增数列,自己尝试使用excel做了个表格,也能看出是递增的,但并不是严格的“单调递增”数列。
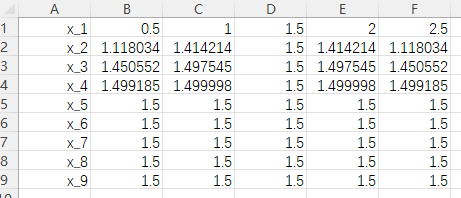
从这个表格中可以看出来,当 \(x_1\) 取大于 1.5 的初始值时,这个数列并不是严格的单调递增数列,例如当 \(x_1 = 2\) 时,构建出来的具体的数列是 \(2, 1.414, 1.497, 1.499, \cdots\),它的 \(x_1\) 到 \(x_2\) 步进时是个减小的过程。
我的困惑是,这样的数列还能被称为是单调低增数列吗?
