题:求极限 \(\lim_{x \to -\infty} x(\sqrt{x^2+100}+x)\)
心路历程:
1、这道题目乍看上去,直观的感觉结果是无穷大,但实际上计算得出的结果却是确定的、而并不是无穷大。至于为什么会有这种直觉与事实的偏差,要好好反思、总结一下;
2、题目中的极限是趋于“负无穷”的,这在实际计算、推导的时候需要注意。
解:
原式 \(\lim_{x \to -\infty} x(\sqrt{x^2+100}+x)\)
= \(\lim_{x \to -\infty} x\sqrt{x^2+100}+x^2\)
= \(\lim_{x \to -\infty} \frac{(x\sqrt{x^2+100}+x^2)(x\sqrt{x^2+100}-x^2)}{x\sqrt{x^2+100}-x^2}\)
= \(\lim_{x \to -\infty} \frac{100 x^2}{x\sqrt{x^2+100}-x^2}\)
= \(\lim_{x \to -\infty} \frac{100 x}{\sqrt{x^2+100}-x}\)
= \(\lim_{x \to -\infty} \frac{100 x \cdot \frac{1}{x}}{\sqrt{x^2+100}\cdot \frac{1}{x}-x\cdot \frac{1}{x}}\)
= \(\lim_{x \to -\infty} \frac{100}{\sqrt{x^2+100}\cdot \frac{1}{x}-1}\)
此时注意到 \(x\) 的取值是在负数、负无穷时刻的,因而有 \(\frac{1}{x} = -\sqrt{ \frac{1}{x^2}}\)
继续推导 = \(\lim_{x \to -\infty} \frac{100}{\sqrt{x^2+100}\cdot \left(-\sqrt{ \frac{1}{x^2}} \right)-1}\)
= \(\lim_{x \to -\infty} \frac{100}{- \sqrt{1+\frac{100}{x^2}}-1}\) = \(\frac{100}{- \sqrt{1+\delta}-1}\) = \(\frac{100}{-1-1}\) = \(\frac{100}{-2}\) = \(-50\)
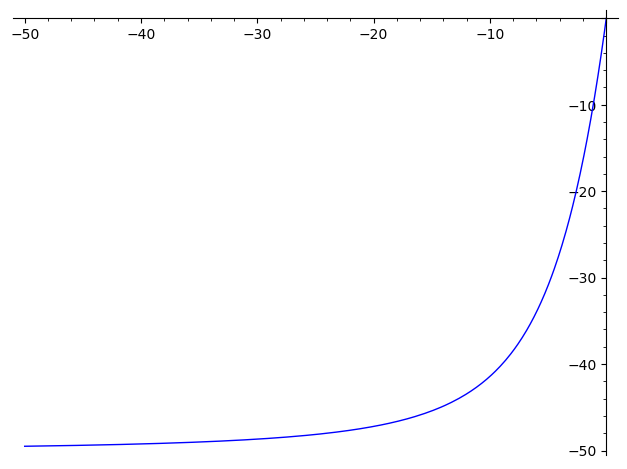
这道题我之所以会觉得有些“不可思议”,是因为按照原式来看,其中只是两个多项式相加,并没有分数、即没有比值的概念,而结果的-50显然是一个“比值、比率”,因而可以断定原始的表达式含有着一个分数形式。虽然推导计算的时候的确构造出了这个分数,但是直观的想,却很难从原式中看出这个“分数”来。这是为什么呢?
实际带入了一些数据发现,我对“极限”的理解是存在误区的:极限并不一定是“比值”,上面结论的-50就不是比值,而是差值:是原始的计算式中两个计算项的差异比较:
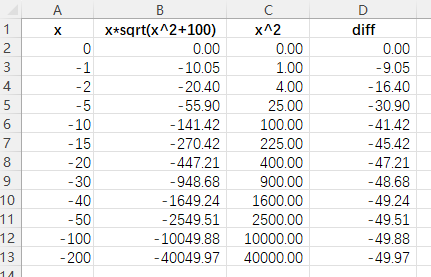
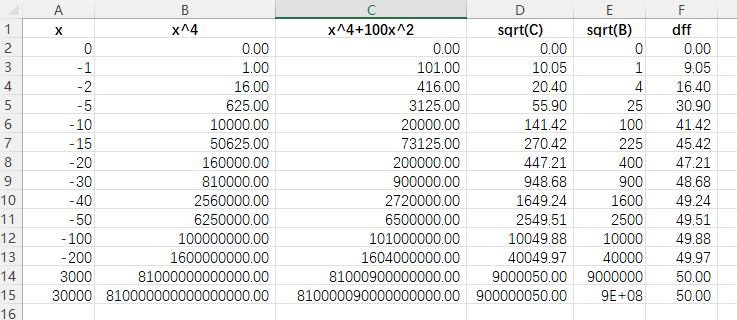
虽然看上去是一个“加法”运算,但是因为 \(x\) 是在负数轴上移动,因而实际上是两个计算式的减法运算。换言之,上面的全部计算可以变换成如下的结论:
\(\lim_{x \to -\infty} -\left( \sqrt{x^4+100x^2} – \sqrt{x^4} \right) = -50\),也就是 \(\sqrt{x^4+100x^2}\) 和 \(\sqrt{x^4}\) 的比较。
但是我还是有些理解不了这个事情,先将数据结论列在这里,等到睡眠充足之后,再慢慢思考这个问题吧。我理解不了的,主要就是C列中的开方符号内那段“多余项”,既然是也在无限增大的,它怎么可能在开方之后就会逐渐的逼近与50这个数字呢?