题:求极限 \(\lim_{n \to \infty} \left[ \sqrt{1+2+\cdots + n} – \sqrt{1+2+ \cdots + (n-1)} \right] \)
解:
1、题目中给出的计算式中含有两个算术级数表达式,但是因为形式上并不是计算通式,所以无法进行后续的推导,所以首先要先写成求和通式形式:
\(\lim_{n \to \infty} \left[ \sqrt{1+2+\cdots + n} – \sqrt{1+2+ \cdots + (n-1)} \right] \) \(=\lim_{n \to \infty} \left[ \sqrt{\frac{(1+n)n}{2}} – \sqrt{\frac{(1+(n-1))(n-1)}{2}} \right] \)2、经过进一步的化简可以得到更简约的极限计算式:
\(\lim_{n \to \infty} \left[ \sqrt{\frac{(1+n)n}{2}} – \sqrt{\frac{(1+(n-1))(n-1)}{2}} \right] \) \(=\lim_{n \to \infty} \left[ \sqrt{\frac{n(n+1)}{2}} – \sqrt{\frac{n(n-1)}{2}} \right] \)3、至此会发现得到的极限计算是一个 \(\infty – \infty\) 形式,无法得到确切的结果。既然当前是 \(\infty – \infty\),那么就设法令其计算因子的位置从分子调整到分母(或从分母调整到分子)上,看一看是否能有改善:
\(\lim_{n \to \infty} \left[ \sqrt{\frac{n(n+1)}{2}} – \sqrt{\frac{n(n-1)}{2}} \right] \) \(= \lim_{n \to \infty} \left[ \sqrt{\frac{n^2+n}{2}} – \sqrt{\frac{n^2-n}{2}} \right] \)根号内计算式分子、分母同时乘以 \(\frac{1}{n^2}\)
\(= \lim_{n \to \infty} \left[ \sqrt{\frac{(n^2+n)(\frac{1}{n^2})}{2(\frac{1}{n^2})}} – \sqrt{\frac{(n^2-n)(\frac{1}{n^2})}{2(\frac{1}{n^2})}} \right] \) \(= \lim_{n \to \infty} \left[ \sqrt{\frac{1+\frac{1}{n}}{\frac{2}{n^2}}} – \sqrt{\frac{1-\frac{1}{n}}{\frac{2}{n^2}}} \right] \) \(= \lim_{n \to \infty} \left[ \frac{n \sqrt{1+\frac{1}{n}}}{\sqrt{2}} – \frac{n \sqrt{1-\frac{1}{n}}}{\sqrt{2}} \right] \)4、至此发现调整之后依然是 \(\infty – \infty\)的形式,并没有得到任何改善,因而上述思路并不顺利。重新观察上述推算,发现在第二步中,有毕达哥拉斯的味道,因而考虑分子、分母同时乘以一个共轭形式:
即:\(\lim_{n \to \infty} \left[ \sqrt{\frac{n(n+1)}{2}} – \sqrt{\frac{n(n-1)}{2}} \right] = \lim_{n \to \infty} \left[ \sqrt{A} – \sqrt{B} \right] = \lim_{n \to \infty} \frac{(\sqrt{A} – \sqrt{B})(\sqrt{A} + \sqrt{B})}{\sqrt{A} + \sqrt{B}}\)
\(= \lim_{n \to \infty} \frac{A-B}{\sqrt{A} + \sqrt{B}} = \lim_{n \to \infty} \frac{\frac{n(n+1)}{2}-\frac{n(n-1)}{2}}{\sqrt{\frac{n(n+1)}{2}} + \sqrt{\frac{n(n-1)}{2}}}\) \(= \lim_{n \to \infty} \frac{\sqrt{2}n}{\sqrt{n^2+n}+\sqrt{n^2-n}}\) \(= \lim_{n \to \infty} \frac{\sqrt{2}n}{n\sqrt{1+\frac{1}{n}}+n\sqrt{1-\frac{1}{n}}}\)5、再对分子、分母约分,即可得到 \(\frac{C}{C+\delta}\) 的极限形式,这个形式是有利于完成极限运算的:
\(= \lim_{n \to \infty} \frac{\sqrt{2}}{\sqrt{1+\frac{1}{n}}+\sqrt{1-\frac{1}{n}}}\) \(= \lim_{\delta \to 0} \frac{\sqrt{2}}{\sqrt{1+\delta}+\sqrt{1-\delta}}\) \(= \frac{\sqrt{2}}{\sqrt{1}+\sqrt{1}}\) \(= \frac{\sqrt{2}}{2}\)至此,计算完成。
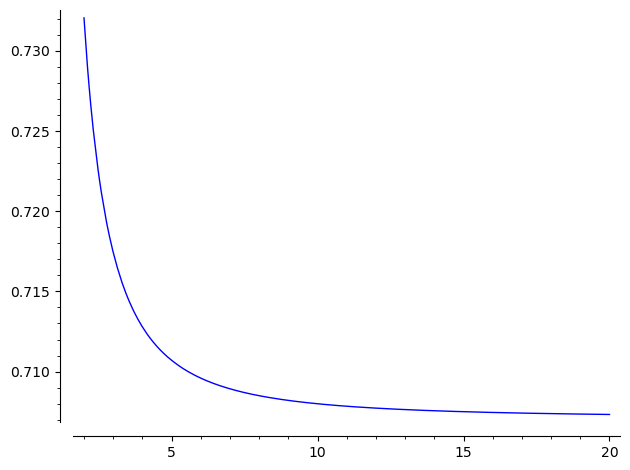
额外的,对于这个问题的图形,用sagemath绘制 \(f(x) = \sqrt{\frac{x(x+1)}{2}} – \sqrt{\frac{x(x-1)}{2}}\) 进行观察,可以发现它的收敛非常快,当 \(x=10\) 时基本就已经逼近到收敛点附近了。