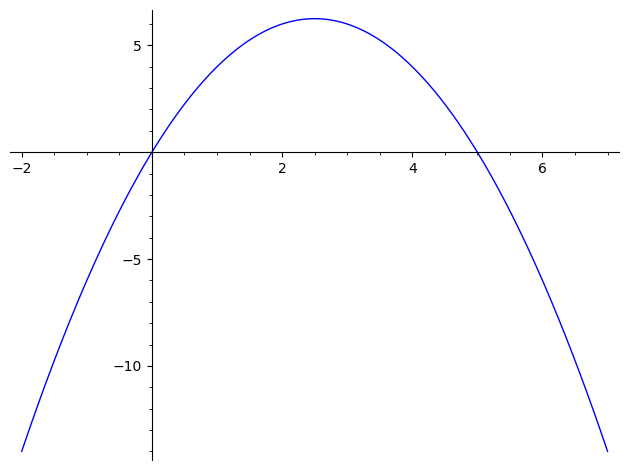
题:求函数 \(y=\sqrt{lg\frac{5x-x^2}{4}}\) 的定义域
解:
1、对于 \(lg \frac{5x-x^2}{4}\) 而言,由对数定义限定导致 \(\frac{5x-x^2}{4} >0\),因而有 \(5x-x^2 > 0\);
2、对于 \(\sqrt{p}\) 而言,由于开方限定导致 \(p \ge 0\),因而有 \(lg \frac{5x-x^2}{4} \ge 0\);
这里1比较容易看明白,2对于刚刚接触指数和对数的我而言有些绕脑子,不妨这么想:
设 \(lg \frac{5x-x^2}{4} = n\),这样就有 \(10^n = \frac{5x-x^2}{4}\),因为 \(n \ge 0\),所以 \(10^n \ge 1\),所以 \(\frac{5x-x^2}{4} \ge 1\)。
整理之后得到 \(5x-x^2 > 0\) 且 \( 5x-x^2 \ge 4\)
最后可以得到同时满足上述两个方程的取值范围也就是原函数的定义域,定义域是 \(1 \le x \le 4\)。