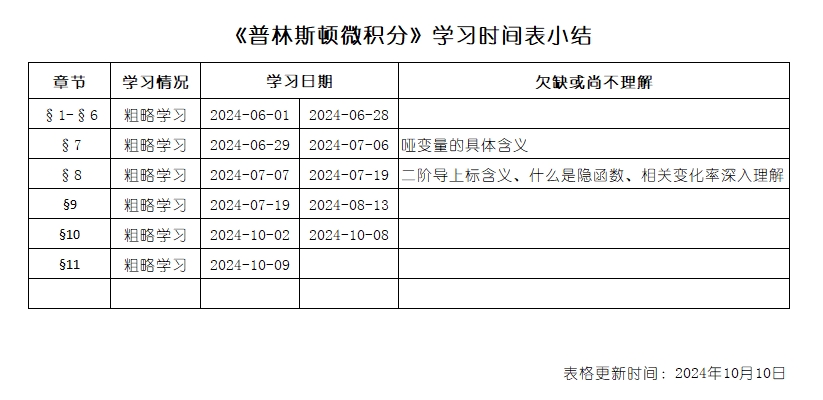
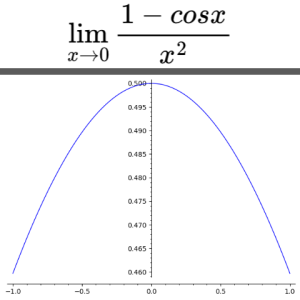
间断了一些时日,终于将《第十章、反函数和三角函数》阅读完了。整体感觉这一章的内容远比前面第九章简单、少很多。所以只花了一周左右的时间就基本粗读完成了。
在阅读这一章的时候有几个比较明显的困难摆在我的面前:首先就是在函数的反函数为什么可以直接通过对原函数的x和y进行对调,就可以得到,这里花了不少的时间,直到现在我也是似懂非懂、一头雾水。
另外就是这一章其实我并没有从始至终阅读完成,其中有几个三角函数我并不了解。前面一些章节中也有类似的情况,当遇到正割、余割时,我都只是囫囵吞枣的看过去;然后在面对双曲函数的时候则是飞快地翻过去的。
如果今后有时间,或者更准确地说如果用到了吧,再学习这块知识。
这一章阅读的过程中,因为自己的电脑升级了、有了更好用的辅助工具,所以配合着软件、工具,也做了更多的上手尝试。这里有两篇这一章的学习笔记:反函数学习笔记(1)、反函数学习笔记(2)。
当完成第十章的阅读时,其实除了上面笔记中的问题,我还存在着另外一个困惑:
这一章的重点究竟在哪里?是在介绍三角函数么?这可是微积分教材呀!所以这一章的重点应该是在介绍:在已知一个函数的前提下,如何计算这个已知函数的反函数的导数。
罗嗦的解释一下就是:已知函数,不求它的反函数的显式形式、避开它反函数的显式定义,而直接求出这个反函数的导数来。这是我的困惑便产生了:既然是在讲解“函数的反函数求导”,为什么全章都在介绍各种三角函数、反复用各种三角函数去完成举例呢?
它为什么不用多项式函数、指数函数、对数函数等举例,而非要一个个三角函数的拿出来,画出他们的反函数、找出这些反函数的导数呢?这有什么特殊的用意吗?或者,是否是因为反函数求导,更多的出现在三角函数领域中?
我现在只能把这个困惑先放一放,姑且认为也许就是因为三角函数的反函数比较常见、特点比较鲜明吧。
无论如何,这一章阅读完成,接下去我将一鼓作气,尽快将这本书的前半部分——微分——阅读完成。