当使用 SageMath 进行函数 \(f(x) = \sqrt[3]{x}\) 的定义并尝试绘制出图形的时候,会遇到警告错误,同时无法得到预期的函数图像:
sage: var('x')
sage: f(x) = x^(1/3)
sage: plot(f)
verbose 0 (3839: plot.py, generate_plot_points) WARNING: When plotting, failed to evaluate function at 100 points.
verbose 0 (3839: plot.py, generate_plot_points) Last error message: 'can't convert complex to float'
Launched png viewer for Graphics object consisting of 1 graphics primitive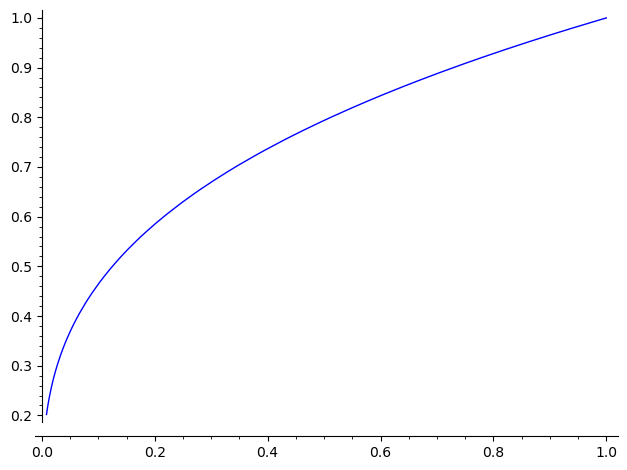
按照 SageMath 给出的 warning 信息来看,它有100个点无法完成正确的绘制。这是因为 SageMath 在进行 plot 绘制图像时,会依函数进行200次采样、得到200个点,并进行图像的绘制。而上面定义出来的函数,在x轴负半轴上无法得到有效的实数计算结果,从而整个x负半轴的100次采样均无法计算出有效的结果,引起的问题。
通过以下尝试带入一些具体的数值计算,可以看出来:
sage: f(1)
1
sage: f(27)
3
sage: f(-1)
(-1)^(1/3)
sage: f(-27)
3*(-1)^(1/3)
sage: f(-1).n()
0.500000000000000 + 0.866025403784439*I
sage: f(-1).real_part()
1/2SageMath 在计算复数的立方根时,并不能得到最终的数值结果,而给出了带有符号的计算式。如果强行通过.n()方法进行转换,也依然无法得到正确的结果——SageMath 会计算出一个复数结果。也正是因为这个原因,导致了它无法在实数域的平面坐标系上完成标点绘图。
SageMath 之所以无法完成对-1开立方根、或者说无法对-1在实数域内完成开立方根,主要原因是:它首先是基于 \((-1)^{\frac{1}{3}}=e^{\frac{i\pi}{3}}\) 进行推导计算;其次是我们使用的计算方法不合理,导致 SageMath 并不清楚我们的计算意图导致的。
解决方案比较多,有简单粗暴的(只考虑结果的正确性、不考虑意图性),也有更加合理的(使用更加正确的计算方法,令 SageMath 了解我们的计算意图以给出预期结果)。
方案一、人为确定符号
这是一个简单粗暴的方案,人为介入的动作比较多,相当于是人工进行了计算式的化简,将符号提前抽取出来,之后由 SageMath 完成正数的开立方操作:
sage: f(x) = sgn(x) * abs(x)^(1/3)
sage: f(-1)
-1
sage: f(-27)
-3
sage: plot(f)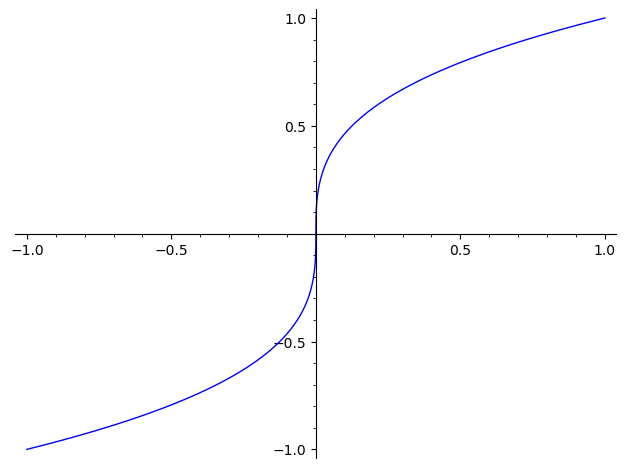
这样做的好处是,纵使对 SageMath 的用法、函数并不是全然了解,也能够按照预期得到计算结果和图形。
方案二、使用实数开方方法完成函数定义
这是更好的方法,可以在自己的函数在定义时便将意图明确出来:我们只期望得到实数结果:
sage: f(x) = real_nth_root(x, 3)
sage: f(-1)
-1
sage: f(-27)
-3
sage: f(27)
3这样定义出来的函数 \(f(x)\) 更加准确的表达了计算意图和定义域、值域的范围,不仅简单明了、也可以令 SageMath 了解计算用途、从而在内部完成更准确的算法选择、提升计算效率。