一、反函数的基本概念:
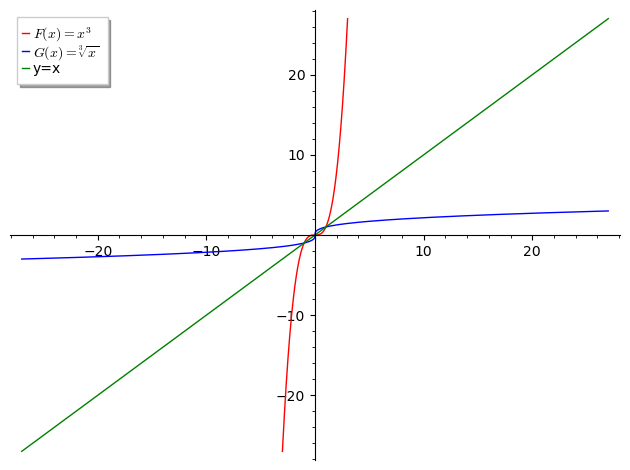
1、最为直观的,一个函数在坐标系上画出来之后,如果有另外一个函数的图像,与它是关于\(f(x)=x\)对称的,那么这两个函数就互为反函数;
2、如果按照定义来说,当有\(f(g(x))=x\),且\(g(f(x))=x\)时,这两个函数就是互为反函数的;
3、例如\(f(x) = x^3\),它的反函数是\(g(x)=\sqrt[3]{x}\),可以从图像上看出来那么的确是关于绿色的线轴对称的:
二、书上的一处描述歧义:
在“一版1印”中的表述:假设,有一个可导函数f,它的导数总是正的。你认为该函数的图像会是什么样的呢?好吧,切线的斜率必定处处为正,故该函数不可能向上或向下倾……
在“二版55印”中的表述:假设有一个可导函数f,它的导数总是正的。你认为该函数的图像会是什么样的呢?好吧,切线的斜率必定处处为正,故该函数不可能上下起伏……
这个“第一版”中有不少这样的表述错误,会令读者在阅读时产生困惑、甚至不解。好在有最新版本对比着阅读,才不至于在它错误的表述上花费太多的时间。
三、使用SageMath绘图时遇到的2个小障碍:
1、SageMath在处理\(g(x) = \sqrt[3]{x}\)时需要人为介入、手动调整符号。如果直接使用下面的代码对\(g(x)\)进行定义,SageMath的计算会考虑到复数情形、而且在画图的时候无法绘制出负数范围部分的图像:
sage: g(x) = x^(1/3)这个时候需要自己对符号进行处理,改成如下的定义形式才能完成正确的计算过程:
sage: g(x) = sign(x) * abs(x)^(1/3)2、当想将\(\)和\(\)两个函数同时绘制出来的时候,需要注意两个函数的定义域范围要分别定义,如果定义在相同的定义域上,绘制出来的图像将很难观察他们两个的对称性:
sage: var('x')
sage: f(x) = x^3
sage: g(x) = sign(x) * abs(x)^(1/3)
sage: p1 = plot(f, (x, -3, 3), color="red", legend_label="f(x)=x^3")
sage: p2 = plot(g, (x, -27, 27), color="blue", legend_label="g(x)=x^(1/3)")
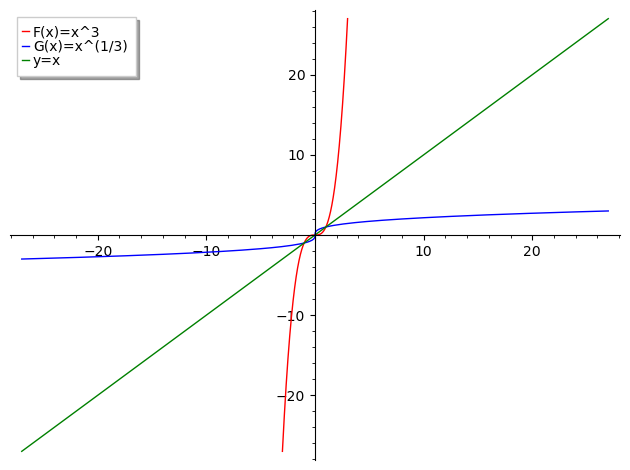
sage: (p1+p2).show()注意f函数的定义域应该取[-3,3],g函数的定义域取[-27,27],这样绘制出来的图像才能比较方便的观察出对称性。我之前两个函数的定义域都设置成了[-27,27],导致观察的时候以为g函数的图象是与x轴平行重合的,错误的观察导致错误的判断、结果以为函数定义出了错误、在这上花了一些时间。
四、手算反函数:
书中使用的例子是\(f(x) = \frac{1}{3}x^3-x^2+5x-11\),并且提到手算这个函数的反函数是很困难的,如果只是为了证明它是否有反函数,可以使用导数、然后判断导数的结果恒大于零,从而确保它是符合平行线检验、从而得出“有反函数”的结论。
但是我还是想要了解、尝试一下手算反函数的方法与过程。
五、SageMath中的图例使用LaTex排版:
sage: p1 = plot(f, (x, -3, 3), color="red", legend_label=r"$F(x)=x^3$" )
sage: p2 = plot(g, (x, -27, 27), color="blue", legend_label=r"$G(x)=\sqrt[3]{x}$" )其中的legend_label可以用r””定义字符串,然后其中使用$$做首尾包裹,包裹中的字符串就是LaTex内容,渲染输出的时候,这部分内容将会依LaTex进行排版渲染。得到的图像会更加精致一些: