无题
设 ,若定义 ,其中 。此时的数列 ,是个递增数列还是递减数列?或者说它并不是单调的? 我看书上说这个数列是一个递增数列,自己尝试使用excel做了个表格,也能看出是递增的,但并不是严格的“单调递增”数列。 从这个表格中可以看出来,当 取大于 1.5 的初始值时,这个数列并不是严格的单调递增数列,例如当 时,构建出来的具体的数列是 ,它的 到 步进时是个减小的过程。 我的困惑是,这样的数列还能被称为是单调低增数列吗?

《第6章:求解微分问题》二刷笔记
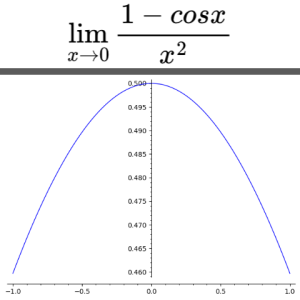
刚刚阅读完第6.1和6.2两篇章节的内容,阅读完成之后我就“慌张”了,因为我忘记了为什么要阅读这两个章节、为什么要“二刷”这部分的内容。好在后来又想起来了。这是一个教训,今后要准备个记事本,将每时每刻的想法都记录下来(年龄大了,记忆力明显出了问题)。 我之所以要二刷这两个章节,原因是之前完成了《普》的粗略学习之后,在这本书中夹入了不少的便笺、记录着自己的困惑和不解。我想等第一遍阅读完成之后,会从头翻阅一遍,将其中所有的便笺找出来,逐一夯实一下。 今天晚上从头翻查,第一张便笺便是出现在第六章中的。但是这张便笺我已经忘记当初写的时候是什么想法了,所以只好又从头阅读。将6.1和6.2阅读下来,之前的便笺内容并没有解决(也可能多少解决了一些),但是却又多出来几个新的困惑,逐一记录,并且期望逐一解决吧。 这是今天新增加的便笺,今天稍后一些的阅读其实已经解答了这个问题。所以一刷的时候不存在这个困惑、二刷完成的时候也不存在这个困惑。这个困惑只在于刚刚阅读到6.1时才会产生。乘积求导法则之所以是这个形式,后面是有解释的,利用了uv视为矩形面积时,d(uv)就是这个面积增量的例子进行了解释。 当然这里我其实还是存在一些困惑的(后面的便笺)中有记录。 这张便笺中第二个问题其实我也存在着困惑,书上对乘积法则、商法则、链式法则,都给出了两种形式版本,但是我却看不出两个版本的区别。有区别吗?在我看来没有区别,只是一个写得正规一些、另一个版本写的相对简化一些,并没有看出这两个版本对于实际解题,有什么本质的区别。 书上给出的三个法则顺序是:乘积法则、商法则、链式法则。在我看来,商法则应该最后给出来才更好一些,原因是商法则可以通过乘积法则和链式法则的合作,推导出来。 这里有一个问题:如果对求导符号理解的不够深刻,在自己尝试推导商法则的时候,往往会注意不到其中的一个细节,忽略了其中隐含的链式求导,只应用乘积法则进行推导,最终推导出错误的商法则。因而理解求导符号、看清楚其中的函数、尤其看清楚函数的自变量,才能发掘其中的链式函数,进而得到正确的结果。(这段描述又是语焉不详的,我甚至能够想见,未来自己再看自己写的这段话时,一定会忘记自己此刻的想法。所以对于这段表述,应该再额外的详细写一下,说明究竟哪里是需要用到链式求导法则的)。 便签下面提到的两个为什么成立,书中稍后便是解释,其中乘积法则的解释上文提到了,利用的面积观察。而链式法则,用到的什么方法我也说不清楚,但此刻我是理解了的,但为了防止今后的遗忘,也要再抽时间总结成文章记录下来。 这张便笺,连同后面原文的第一句话、铅笔备忘、下面的蓝色备忘,对我而言都是一个事情:我始终不理解微分符号究竟是个整体、还是个因子。书上此刻说它是个整体,但在实际做题时往往会被他们当成因子看待,这是什么原因? 这张便笺也是我的一个朦朦胧胧的困惑,为什么微分中高阶无穷小是可以被忽略掉的?怎么就被忽略掉了?上大学的时候这里我就没有搞清楚,稀里糊涂的混过去了,如今还是不清楚,所以也只好再次记录下来,期待接下来的日子里,能把这个细节搞搞明白。
《普林斯顿微积分读本》(27、28、30章)及一刷小结
今天基本将《普斯林顿微积分读本》从头到尾阅读完了一遍,只是粗略的阅读,如果接下来的时间允许,将会再次从头重新夯实一遍。 整本书一共是30章,其中第29章《体积、弧长和表面积》我并没有阅读:一方面是对这个话题不感兴趣;另一方面也可能是临近结尾,我总想着尽快将全书读完,所以有一些心浮气躁了。 这种“心浮气躁”也体现在对地28章、30章的阅读上,其中有很多的困惑,并没有花时间推敲、也没有动笔计算。只是看了几遍,大题感觉到推导或解决的过程,便草草结束了。 之所以比较着急,是因为我想着先完成“粗略学习”这个过程,然后返回头去再重新阅读一遍。所以接下来将重新学习这本教材,并且找一些练习题跟着做一做、练一练,争取将有关微积分入门的知识掌握下来。 我甚至都快忘记为什么要重读“微积分”这门课程了,之所以心血来潮地重学微积分,是有两个想做的视频话题中牵扯到了一些微积分的知识: 1、在模拟电路中,比较常见的微分电路和积分电路,为什么这些电路会被命名为微分电路和积分电路呢? 2、在之前阅读有关Kilby的历史故事时,谈到他发明、创造的集成电路工艺,其中有一个初期电路中,涉及到了微分方程的求解。 所以我是因为上面两点,才重新回顾了一下微积分的话题,但是现在微积分看完了,上面两个话题当初是怎么读到、有什么困惑,现在似乎又忘记了……恐怕还要回过头再翻日记,才能回忆起来。
级数、泰勒级数(22章-26章)学习小结
又花了几天的时间将第22章-26章阅读了几遍,确定的说应该是反复阅读了3遍。因为缺少例题、缺少实际的感性认知、缺少动笔,所以这5章的内容读起来不困难、但是却很难在头脑中勾勒出清晰的知识框架。总是有一种似懂非懂、囫囵吞枣地感觉。 之所以如此朦胧,我觉得上面提到的诸多原因是原因,此外还有一些原因: 首先是无论手中的电子版、还是纸质版,这几章的内容无论是从文字的表达上、还是翻译的质量上,都不如全书前面章节那么清晰。尤其一些表述,指代的非常含混。 另外一方面就是跳跃性实在有些大:既有某些基础知识是前面介绍的,又有很多没有的知识作者埋下伏笔要等后面学习之后才能明确。这样的反复跳跃导致阅读者思路难以连贯。 再加上这几章的计算式中数学符号和数字明显更多,对于业余学习数学的我而言有一些眼花缭乱。 总之这几章的学习只能说是“阅读完”,不能说是“掌握”。 好在眼见着整本书即将全部阅读完成,这至少给了我很大的成就感。等全书的“粗略学习”完成之后,可以再从头学习一遍、甚至两遍,这样应该能够夯实现在似懂非懂的知识。 其实在学习过程中也做了不少的笔记,但是始终没有时间和精力整理成博客文章。等到“二刷”这本书的时候,要将所有的笔记整理出来,这样应该会对自己的学习更有效果。现在有一些跃跃欲试,急不可耐了呢。
积分(15-19章、20-21章)小结
一口气将微积分的第15-19章全部阅读下来,整体感觉并不难,至少读起来不难。手中这本《普斯林顿微积分》应该说是入门教材,而且习题很少,所以相对来说阅读的十分轻松。 不过仍然能够感觉到:积分一定是比微分更难的,只不过因为我没有做题,所以从理解的角度上看,积分反而比微分容易了一些。 如果有习题,那么积分部分的例题肯定是困难的,主要原因在于积分并不像微分那么直观,任何一道积分的习题,估计都是需要通过观察以及大量的积累,才能快速的找到解题途径。否则无论怎么尝试,路径不对,都很难得到有效的简化途径完成解答。 但是我现在想的是尽快完成这本书的阅读,然后再返回头来做题,毕竟手中已经挤压了不少其他的书籍,这本“厚重的”图书不阅读完,其他图书就不敢翻开开始阅读。所以还是以读为主,至于例题呢,放到全书阅读完成之后,我想可以养成一个“每日一题”的习惯来做一做。 上面是15-19章的学习小结,但是似乎也没有“小结”出任何的内容来,主要原因是这些章节的内容在我看来都是“介绍性”的,一边阅读一边就了解了。并没有动笔计算,所以也就没有太多的困惑值得记录。 接下来的20章和21章似乎也是如此——有关反常积分的概念和具体的计算方式。所以依然没有花费太多的时间,只是一行行的阅读着就完成了两个章节的学习。 反常积分这两个章节我在阅读的时候还是有一些小困惑的: 1、反常积分在之前上学学习微积分的时候并没有学习,如今应该是第一次接触到。所以我的困惑就是这种“反常积分”计算,究竟是在什么样的应用领域中才会遇到呢?书上说工程上非常常见,但是因为自己没有相关的经验,所以并不了解具体的应用案例。 上网搜索了一下,看到一种比较常见的情况:在电磁学中,信号的发生通常是会形成震荡的,这个时候可以将这个震荡的信号看作是t区域∞的反常积分,通过计算可以知道这一信号从产生到∞的时间范围内,对整个电路系统产生的“能量”大小。从而评估出信号的稳定性。 2、另外一个困惑就是书上在介绍反常积分的时候提到:只要完成对积分结果是收敛还是发散的判定就可以了,而无需对具体的结果数值进行计算。 这又让我觉得有些困惑:既然都已经判定出收敛性了,为什么不继续计算,将最终的结果计算出来呢?也许是因为对于大多数反常积分,想计算出最终的结果比较困难么?依然是通过网络搜索找到一些可能的答案: 首先是的确可能计算困难,有些反常积分如果一定要计算出最终的收敛结果,可能需要用到留数定理、数值积分等更高级的数学工具,而在本科阶段的微积分课程中,这些数学工具还没有学习; 另外一方面,在工程应用上,完成反常积分的收敛性判定就可以得到期望的结果:物理量的收敛与否决定了系统的稳定性和可行性。完成这一步的判断就已经可以为工程进行指导,而无需关心最终的收敛数值结果。 无论如何,这两章也算是阅读完成了,看着手中这本教材逐渐变薄,心中还是十分喜悦的。
微分(12、13、14章)学习笔记
今天一天完成了微分章节的“第12章-第14章”的阅读,相比之前各个章节的阅读速度,这三章阅读起来显然是快了许多。但这并不能说明我的头脑已经适应了数学、只是因为这三章的内容比较少,相对容易阅读和理解。 第12章、绘制函数的图像 我在阅读这一章的时候,心中总是想着用sagemath能够方便的完成函数图像的绘制,所以有一些放松警惕,完全没有深入思考书中的每一个细节。实际上如果真想将一个函数准确的、正确的、按照书中的步骤绘制出来,恐怕对我而言还是非常难的。 第13章、最优化和线性化 这一章的内容相对来说是我比较感兴趣,觉得有意思、有趣的。它可以解决实际的问题,而且让我感受到利用导数寻找最优化数值的神奇。 第14章、洛必达法则及极限问题总结 这一章其实是分成两部分的。首先是对于一些极限表达式,如果符合洛必达法则的规则,便可以通过洛必达法则对其求解极限。第二部分则是对求极限问题的一个归纳和小结,将当前14章知识中所有可以用于求极限的手段进行了归纳。 其中洛必达法则作为常用的求极限手段,给出了若干的例题。我囫囵吞枣地跟着书上的内容看了一遍,但是既没有动笔动手跟着计算、也没有额外找来其它练习题自己进行独立推敲。 所以如果后期有时间了,我想这块内容还是要再花时间重新温故、稳固。 无论如何,今天感觉还是很开心的,终于将手中的这本微积分读物完成了50%的阅读。接下去将开始下半场旅程——继续后面积分部分的阅读和学习。
《导数和图像》(11章)学习笔记
一、上一章遗留的一个小问题: 这一章整体阅读完成之后,算是将上一章遗留的困惑搞清楚了一些: 假设有一个可导函数 f ,它的导数总是正的,它的切线的斜率必定处处为正,故该函数不可能上下起伏,该函数一定是递增的。在第11章将证明这个事实。不管怎样,如果函数 f 总是递增的,那么它一定满足水平线检验。 第10章开始处的一段话 就是上面这句话,出现在第10章的开始处,我是读了好几遍也没有明白“这个事实”指的是“哪个事实”。所以索性就把这段文字中所有可能是“事实”的事情都先罗列出来吧: 1、如果可导函数 f 的导数是正的,该函数一定是递增的; 2、如果函数 f 总是递增的,那么它一定满足水平线检验。 而在第11.2章节中提到: 下面举一个罗尔定理应用的例子:假设有一个函数 f 满足 f’ (x) > 0 (对于所有的 x),在 10.1.1 节中,我们断言该函数一定满足水平线检验。…
《反函数和三角函数》(10章)学习笔记
间断了一些时日,终于将《第十章、反函数和三角函数》阅读完了。整体感觉这一章的内容远比前面第九章简单、少很多。所以只花了一周左右的时间就基本粗读完成了。 在阅读这一章的时候有几个比较明显的困难摆在我的面前:首先就是在函数的反函数为什么可以直接通过对原函数的x和y进行对调,就可以得到,这里花了不少的时间,直到现在我也是似懂非懂、一头雾水。 另外就是这一章其实我并没有从始至终阅读完成,其中有几个三角函数我并不了解。前面一些章节中也有类似的情况,当遇到正割、余割时,我都只是囫囵吞枣的看过去;然后在面对双曲函数的时候则是飞快地翻过去的。 如果今后有时间,或者更准确地说如果用到了吧,再学习这块知识。 这一章阅读的过程中,因为自己的电脑升级了、有了更好用的辅助工具,所以配合着软件、工具,也做了更多的上手尝试。这里有两篇这一章的学习笔记:反函数学习笔记(1)、反函数学习笔记(2)。 当完成第十章的阅读时,其实除了上面笔记中的问题,我还存在着另外一个困惑: 这一章的重点究竟在哪里?是在介绍三角函数么?这可是微积分教材呀!所以这一章的重点应该是在介绍:在已知一个函数的前提下,如何计算这个已知函数的反函数的导数。 罗嗦的解释一下就是:已知函数,不求它的反函数的显式形式、避开它反函数的显式定义,而直接求出这个反函数的导数来。这是我的困惑便产生了:既然是在讲解“函数的反函数求导”,为什么全章都在介绍各种三角函数、反复用各种三角函数去完成举例呢? 它为什么不用多项式函数、指数函数、对数函数等举例,而非要一个个三角函数的拿出来,画出他们的反函数、找出这些反函数的导数呢?这有什么特殊的用意吗?或者,是否是因为反函数求导,更多的出现在三角函数领域中? 我现在只能把这个困惑先放一放,姑且认为也许就是因为三角函数的反函数比较常见、特点比较鲜明吧。 无论如何,这一章阅读完成,接下去我将一鼓作气,尽快将这本书的前半部分——微分——阅读完成。
反函数学习笔记(2)
一、什么要在后面进行证明? 这一章开始就有一句话是我始终无法理解的:“我们会在下一章证明这个事实”,这句话中的“这个事实”是什么呢? 二、“一种方法”我理解不了 如截图所示,书中给出的对“正弦函数的反函数”进行求导,提到了使用“一种方法”,这个方法我现在理解不了、头脑一片混乱。 在稍微往前一点的章节中,作者用到的也是如上形式相同的方法进行某个函数的反函数求导,都是“这种方法”,我理解不了的原因主要在于: 1、有些绕脑子,无法理解为什么x和y彼此对调一下就能直接使用了;2、它没有个更正式的名称么? 但是好在,我找到了“另一种方法”,更加容易理解。但是因为篇幅有限(使用LaTex在blog中排版实在太麻烦了,所以暂时就先做这样一个不伦不类的备忘,等到后期有时间了,再重新整理、补充上来吧)。 2.1、我似乎理解了作者的解法(update: 2024.10.09) 首先,作者使用的这个解法,正式的名称应该是“隐函数求导法”,具体的思路是:1、首先依据原函数,构建出它的反函数的“隐式形式”;2、然后不对“隐函数”进行整理、不得出它的“显式形式”;3、直接进行“隐函数求导”就可以了;4、最后再稍作整理,将其中的y值设法用x值表示出来。 我之所以无法理解它,主要是因为从原函数到反函数的变化过程、或者说反函数的定义过程,没有理解。例如: 原函数如果是:,如果想对这个原函数的反函数求导,首先就是要找到、或者定义出它的反函数来,但是要怎么定义它的反函数呢?直接通过下面的方法构建出来隐函数方程,并且不进行简化就可以了: 原函数: 反函数的隐式表达形式: 这就是隐函数,虽然没有得出一个显式的表达式,但是直接用这个隐函数求导就可以了。作者的解法我虽然理解了,但还是绕脑子、吃不透、无法顿悟,痛苦中。我想我最大的困惑就是为什么只需要将x和y对调一下位置,就可以定义出反函数来了? 2.2、再次尝试理解反函数 原函数:,我换一种写法,将x写成“输入”、将y写成“输出”,看这样是否能够避开抽象的符号,让自己的头脑更清晰一些? 原函数:,这个原始的函数的目的是:通过给定一个具体的输入值、经过某种映射关系,得到一个明确的输出值。 现在抛开x和y的想法,只是将上面的等式稍作调整、只是文字上的调整,调整成,不用关心文字细节的变化,他们本质上还是喂入一个具体的输入数值、经过同样的映射、得到经过映射之后的输出数值。 此时对于调整后的关系式:既可以说它的自变量是,经过正弦映射得到计算结果。也可以说自变量是,经过某种未知未解的映射关系,得到的结果将是。如果按照后面的说法来说,那么上面的关系式就变成了一个未解、待解的方程,需要求解出来,才能看出具体的映射关系来。 至此,如果不求解,那么上面的未解方程,就已经是一个隐式函数了;若能解出来,那么就是显式定义的函数。 2.3、适用于我自己的方法(其实这个方法也有个更准确的名称:基于反函数性质的求导法) 上面的“对调x和y其实我还是一头雾水”,先这样吧。接下来记录一下自己比较能够理解的方法。但是自己用的这个方法似乎也存在缺陷,在“教材”后面专门提到过,似乎是要注意f(r(x))和r(f(x))两种不同的嵌套关系中,一种是错误的、一种是正确的;我还没有时间详细推敲我所使用的这个建议的推导过程,是否正中了教材中明确指出的错误。 提问:已知正弦函数,求其反函数的导数。 解: 首先定义的反函数为,欲求。这里之所以不使用原因是相似符号太多眼睛容易花。 因为根据函数与反函数的特性,有…
SageMath 使用问题一则
当使用 SageMath 进行函数 的定义并尝试绘制出图形的时候,会遇到警告错误,同时无法得到预期的函数图像: 按照 SageMath 给出的 warning 信息来看,它有100个点无法完成正确的绘制。这是因为 SageMath 在进行 plot 绘制图像时,会依函数进行200次采样、得到200个点,并进行图像的绘制。而上面定义出来的函数,在x轴负半轴上无法得到有效的实数计算结果,从而整个x负半轴的100次采样均无法计算出有效的结果,引起的问题。 通过以下尝试带入一些具体的数值计算,可以看出来: SageMath 在计算复数的立方根时,并不能得到最终的数值结果,而给出了带有符号的计算式。如果强行通过.n()方法进行转换,也依然无法得到正确的结果——SageMath 会计算出一个复数结果。也正是因为这个原因,导致了它无法在实数域的平面坐标系上完成标点绘图。 SageMath 之所以无法完成对-1开立方根、或者说无法对-1在实数域内完成开立方根,主要原因是:它首先是基于 进行推导计算;其次是我们使用的计算方法不合理,导致 SageMath 并不清楚我们的计算意图导致的。 解决方案比较多,有简单粗暴的(只考虑结果的正确性、不考虑意图性),也有更加合理的(使用更加正确的计算方法,令 SageMath 了解我们的计算意图以给出预期结果)。 方案一、人为确定符号 这是一个简单粗暴的方案,人为介入的动作比较多,相当于是人工进行了计算式的化简,将符号提前抽取出来,之后由…