一、之前的学习笔记整理：

学习笔记	内容简述及收获心得
RC振荡电路初学笔记（1）	关于Jack·Kilby发明集成电路，并且这个电路是RC相移震荡电路的引子
RC振荡电路初学笔记（2）	关于Jack·Kilby发明集成电路的历史趣闻
RC振荡电路初学笔记（3）	罗列了几点RC相移电路中的个人困惑和备忘
RC振荡电路初学笔记（4）	对Jack·Kilby为什么使用PNP而非NPN做震荡电路做了些毫无根据的猜测
RC振荡电路初学笔记（5）	通过仿真软件对RC电路具体参数确定时的正确输出频率做了仿真

二、电容电流超前于电容电压的原因：

书上的解释是：只有对电容器充电之后，电容器内部有了电荷，电容器两端才有电压，所以流过电容器的电流是超前于电压的。如上的这个表述我是万分的无法理解和接受，电流和电压是同时产生的，怎么可能有谁超前、谁滞后的说法呢？

在物理世界中，电压与电流应该就是彼此同时产生、同时消失的，不会有电流超前于电压的“预知”能力（如果特别特别较真儿、我觉得也应该是先有电压才能驱动产生电流，但他们二者的因果时序近乎于瞬时，所以不能用可评估的时间去表述谁先谁后。所以无论如何也没有道理说出电流超前于电压这种话来）。更准确的表述应该是：电容器上的电压变化率引起了电容器上的电流产生，而电容器上的电压波形与电流波形在同个坐标系上比较，是相同的正弦波形，但相差着90°的相位差。

以最简单的一个理想电容器举例，图样就是一颗电容器画在纸面上：

这个时候电容器内部无论带有多少电荷，它的电荷量都不会随着时间发生变化，因而电容器上不会产生电流。当外部向电容器输入电荷、或者电容器向外部输出电荷时，随着电荷的增加或减小，电容器上同时的表现出了电压的波动和电流的产生。

因为电容器的电流 \(I_C = \frac{dQ}{dt} = C \frac{dV}{dt}\)

所以电流的波动和电压的波动是同时因为电荷的增减而同时引起的。

而又依然是通过上式可以看出来：在外部存在一个正弦电压施压在电容器上时，电容电压的变化频率就是电源电压的变化频率，所以电容电压 \(V_C = V_C^{max} sin(\omega t)\)

电容电流 \(I_C = C \frac{d}{dt} (V_C^{max} sin(\omega t)) = \omega C V_C^{max} cos(\omega t) = \omega C V_C^{max} sin(\omega t + \frac{\pi}{2})\)

此时就能看出来电容上的电压与电流相差90°的关系来了。

额外的，还可以用另一个更简单的解释来说明二者存在着90°的相位差。依然是通过观察电容器的电流 \(I_C = \frac{dQ}{dt} = C \frac{dV}{dt}\)。能够想到的是其中的电压V是个正弦波形态，那么在这个波形的极值点上的导数是0，所以这些极值点时对应的电流就是0，而在x轴过零交点上的导数最大（变化率最大），因而过零点时刻的电流最大。

上面这个关系说明了：电压最大时（正、负极值）、电流最小；电压最小（电压=0v）时的电容器充放电流最大。这与物理常识并不矛盾。电压最大时，在dt时间范围内电压却不再发生变化，所以没有电压的变化就没有电流；过零点虽然电容器上不存在电压，但是这个时候却是外界对它施压最大的时刻，最大的电压当然会获得最大的电流。

如上的解释，在我看来更准确一些。而且说明了结论：在电源输出正弦交流电、施压在电容器上时，电容器上的电流与电容器上的电压，是存在着90°的相位差；并且从数学的角度看待：电容器上的电流是超前于电容器上的自身电压、并且是超前90°相位角的。

三、RC相移角的计算方法：

有了电容器的电流超前于电压90°相位角的基础概念之后，就可以看RC相移器了。简单的一组RC相移器有RC滞后器和RC超前器两种组态：

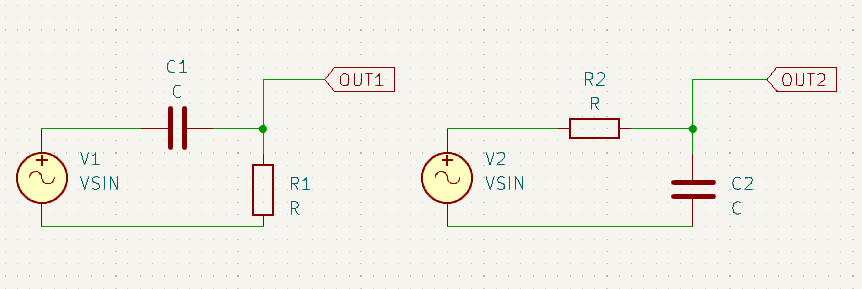
其中左图为超前器、右图为滞后器。这两种组态要讨论的是电压输入点和电压输出点的相位关系。它与上面提及的“电容器自身的电流与电压相位关系”不同，这里要讨论的是\(V_{in}\)和\(V_{out}\)二者的相位关系。

【todo 这里缺少容抗引起相位变化的进一步解释】

Jack·Kilby当年的电路使用的是滞后器网络，今天常见的则以超前器多为常见。索性我就罗嗦一些，分别将二者都罗列出来。实际上这二者只要理解一个，另外一个也就不言自明了。

先看左边的超前器，有两种计算方法可以计算出out点相对于in点的相位角。一种方法是简单且主流的阻抗复数计算法；另外一种则是不引入复数概念、纯粹依据欧姆定律进行微分方程求解。下面依次完成每一种方法的推敲：

• 3.1、超前器复数阻抗计算法；
• 3.2、超前器微分方程求解法；
• 3.3、滞后器复数阻抗计算法；
• 3.4、滞后器微分方程求解法；

3.1、超前器复数阻抗计算法：

因为out点相对于in点的相位角 \(\theta = arc tan \frac{阻抗虚部}{阻抗实部} = arc tan \frac{容抗值}{电阻数} = arc tan \frac{Z_R}{Z_C}\)

又因为电路中的阻抗 \(Z = Z_R + Z_C = R_R – jX_C\)

其中 \(R_R\)就是电阻的阻值，容抗则是 \(X_C = \frac{1}{\omega C}\)

将以上关系式联立即可求出相位角。这个计算方法简单，但并不直观。尤其是对于复数没有概念、或纵使对复数、容抗有概念却依然难以通过直观的电压、电流关系想清楚其中的客观物理原因。所以从思路上更简单的是下面使用的欧姆计算法。

3.2、超前器微分方程求解法：

抛弃复数的概念和容抗的思想，就只用中学物理的知识、即只是用欧姆定律，也是可以完成out点相对于in点相位角计算的，具体过程如下。

电源电压是完美的正弦输出（对于电源而言是输出、对于电路而言电源相当于输入点），那么电源电压就是随着时间不断变化的，它是时间t的函数，因而电源电压的函数式是：\(V_S = U_{in}(t) = U_{in}^{max} \cdot sin(\omega t)\)

输出点与输入点的电压是完全跟随的，只与输入点电压有2点不同：1、因为电路中的电阻形成的电压分压导致输出点电压存在压降；2、因为电容的容性特征引起的输出点电压的相位偏离。

压降的存在是一定的，这是通过欧姆定律就可以判断出来的。而相位偏离就是相位角，我们虽然知道它是存在的，但此时此刻以当前的推导思路而言并不能知道它的存在，所以先假设存在一个相位差，并将其设置成未知量，去设法求解这个位置量。如果求解出来是0，意味着并不存在这样的相位差；如果求解出其他数值，就意味着的确是存在相位差的。

在上面的想法引导下，写出out点的电压随时间函数 \(V_{out} = U_{out}(t) = U_C^{max} \cdot sin(\omega t + \theta)\)

上面的 \(U_C^{max}\) 和 \(\theta\) 都是不知道具体数值的，前者虽然不知道具体数值，但是肯定它是有、并且小于电源电压的；后者只是假设存在，要通过计算的出来看是否是0、或者是真实存在的。

依据欧姆定律，回路中电流时时处处相等。因而电流 \(I = I_R = I_C\)。又可以根据电容上的电流计算式完成电流的计算。电容上的电流 \(I_C = \frac{dQ}{dt} = C \frac{dV_C}{dt}\)。这个电流在回路中完成所有的电压降，因而根据基尔霍夫电压定律 \(U_S = U_R + U_C\) 就可以将以上所有关系式联立到一起。

带入关系式完成联立，最终得到：\(U_{in}^{max} \cdot sin(\omega t) = I_C R + U_C^{max} \cdot sin(\omega t + \theta)\)

带入的更进一步：\(U_{in}^{max} \cdot sin(\omega t) = RC \frac{d}{dt} (U_C^{max} \cdot sin(\omega t + \theta)) + U_C^{max} \cdot sin(\omega t + \theta)\)

上面公式虽然复杂，但简而言之就是 \(f(t) = \frac{d}{dt} g(t) + g(t)\)，如此看来它就是个一阶微分方程。求解就可得解。首先整理、微分；然后利用三角函数两角和对整个式子进行展开；最后求解：

\(U_{in}^{max} \cdot sin(\omega t) \\= RC \frac{d}{dt} (U_C^{max} \cdot sin(\omega t + \theta)) + U_C^{max} \cdot sin(\omega t + \theta) \\=RCU_C^{max} \omega cos(\omega t + \theta) + U_C^{max} sin(\omega t + \theta) \\ = RCU_C^{max} \omega (cos(\omega t)cos(\theta) – sin(\omega t)sin(\theta)) + U_C^{max} (sin(\omega t)cos(\theta) + cos(\omega t)sin(\theta)) \\ =RCU_C^{max} \omega cos(\omega t)cos(\theta) – RCU_C^{max} \omega sin(\omega t)sin(\theta) + U_C^{max} sin(\omega t)cos(\theta) + U_C^{max} cos(\omega t)sin(\theta) \\ = ( U_C^{max} cos(\theta) – RCU_C^{max} \omega ) sin(\theta) sin(\omega t) + ( RCU_C^{max} \omega cos(\theta) + U_C^{max} sin(\theta) ) cos(\omega t)\)

分析系数，即可得到两个独立的方程：

（1）\(U_C^{max} cos(\theta) – RCU_C^{max} \omega ) sin(\theta) = U_{in}^{max}\)

（2）\(RCU_C^{max} \omega cos(\theta) + U_C^{max} sin(\theta) = 0\)

其中的方程（1）容端电压与源电压的关系式，暂时先不讨论。方程（2）是容端相位相对于源相位的关系是，求解此方程，即可知：\(\frac{sin \theta}{cos \theta} = RC \omega = tan \theta\)。

注：这里推导出问题了，应该是上面符号有错误，实际应该是\(\frac{sin \theta}{cos \theta} = \frac{1}{RC\omega} = tan (\theta)\)。

最终得到之前设定的 \(\theta = arc tan(\theta)\)。至此就可以看出来相位角的确存在，并且是与电路中的电阻、电容、电源频率存在关系的。

使用欧姆定律方法完成相位角的求解，可以避开复数概念的引入。整个过程更加的清晰，并且更加的直观。但是这一方法的弊端就是计算起来比较的繁琐，繁琐就容易出错。你看我就在推导过程中出错了不是？

其实有了这两个方法的理解，并且尝试了超前器的推导就已经足够理解RC相移得了。但是Jack·Kilby当年使用的是滞后器组成的移相网络，而且上面所有的推导都没有带入具体的R、C、f数值，因而下面再重复一遍，并且是带入具体数值进行计算。以便加深了解。

3.3、滞后器复数阻抗计算法：

上面已经完成了超前器的相移角计算，接下来再计算一下滞后器，因为超前和滞后几乎没有任何区别，因而没有必要再重复一遍上面的推论，直接带入具体的数值计算即可。

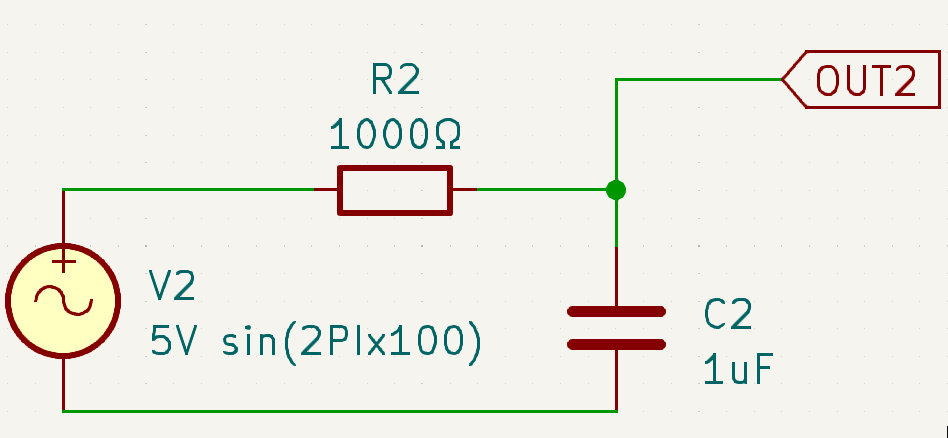
首先计算电路中的阻抗（阻抗=电阻+容抗）。

电阻 \(R = R_R = 1000Ω\)

电抗 \(X_Z = X_C = j \frac{1}{\omega C} = j \frac{1}{2 \pi \cdot 100 \cdot 10^{-6}} Ω\)

相位角 \(\theta = arc tan(\frac{Im}{Re}) = arc tan(\frac{5}{\pi}) = 57.87°\)

这个角度虽然接近60°，但是在100Hz的电源发生器作用下，并非完美的60°。如果想得到一个完美的60°移相，则可以利用上面的计算式，翻转往回计算。例如固定频率、电阻，期望得到60°移相，则可以反推回需要的电容容值是多大。

期望得到的相移角度 \(\theta = 60°\)

即 \(\theta = arc tan(\frac{Im}{Re}) = 60°\)，那么 \(\frac{Im}{Re} = tan(\frac{\pi}{3}) = \sqrt{3}\)

由此往回倒推可知需要电路中的容抗 \(Im = \sqrt{3} \cdot Re = 1000 \sqrt{3}\)

进而根据关系式 \(\frac{1}{2\pi 100 C} = 1000\sqrt{3}\)

最终确定选用的电容容值 \(C = \frac{1}{2\pi 100 \cdot 10^3 \sqrt{3}} = 0,919uF\)

3.4、滞后器微分方程求解法：

已知电阻、电容、角速度的前提下，直接使用3.2得出的结论计算，相位角是 \(\theta = arc tan(\frac{1}{\omega R C} = arc tan (\frac{1}{2\pi 100 \cdot 1000 * 10^{-6}}) = arc tan (\frac{5}{\pi}) = 57.87°\)

这与3.3通过复数方式得到的结果是一致的。至于期望目标相移、反推器件参数，就不再额外记录了。最后给出使用0.919uF电容以期获得近乎完美的60°移相的仿真，为了便于观察，使用三组移相器串联，这样就能看出输入波形与输出波形是呈现180°相位差的了。

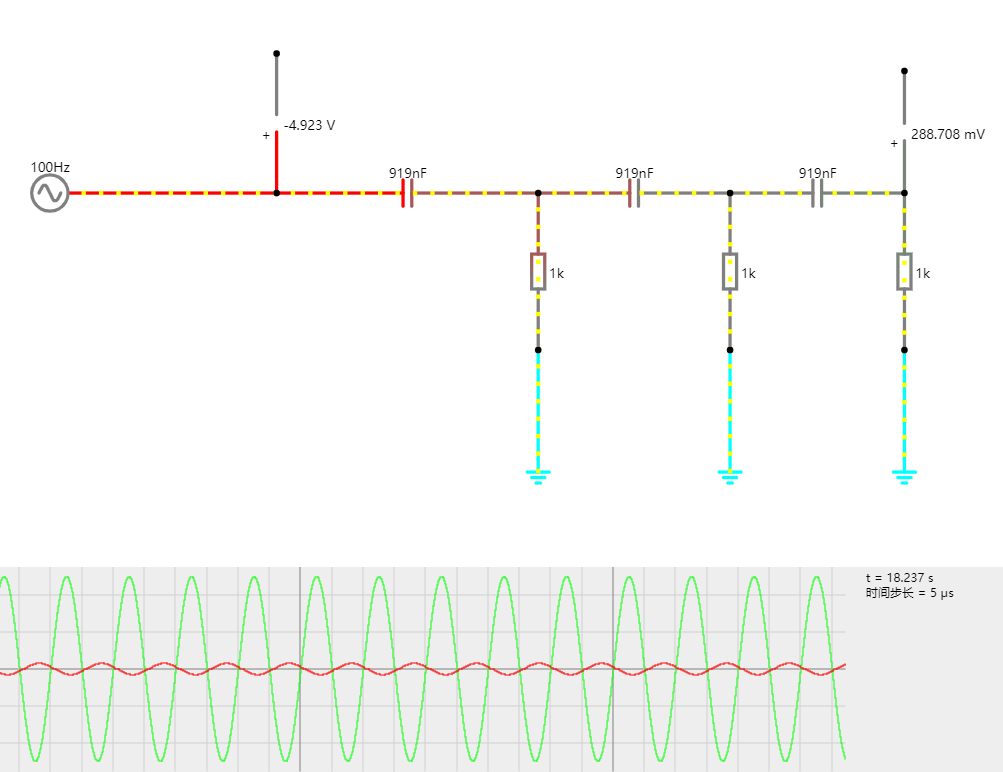
当然还可以使用6组，获得360°相位差，这样观察起来更加的直观，因为输入输出的正弦会出现相位重合。但是之所以不做6组串联观察，是因为经过多次RC相移，输出电压的峰值会越来越低、最后趋于“毫无波澜”，反而看不出结论。

至于每次经过RC相移器之后电压峰值损失，恰是上面3.2中微分方程求解时获得的第一个方程式所能体现出来的，这将在之后再慢慢推敲。