一、我的困惑和不解
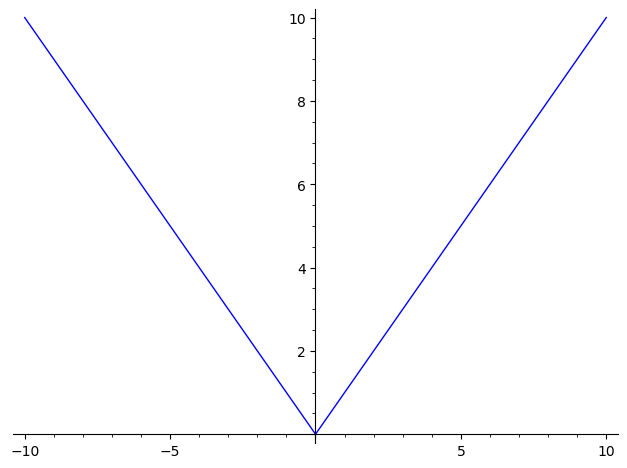
函数\(f(x) = |x|\)的图像如下,显然的,在原点处是没有这个函数的切线的。但这里“显然”似乎又不是那么“显然”,切线究竟是什么呢?对于在平面上的曲线的切线,历史上有过多种定义方式,现今对切线的定义与莱布尼茨给出的定义表述是一致的,都是利用极限的思想对切线进行定义。
对于曲线S上的某一点A,在A点外做另一个同样落在曲线S上的点B,这样AB可以构成一条直线L,这条直线L可以称为曲线S的割线。
当B点沿曲线移动、并逐渐向A点接近,也就是B沿曲线S像A点逼近,当\(\lim B \to A\)时,得到的割线便是经过A点的曲线的切线。
上面的定义本来能够解答下面这个图象的疑问:为什么在\( f(x) = |x| \)图像的原点处,没有切线呢?答:因为如果设原点处为A,可以从图像上看出来,B点在左边和B点在右边两种情况下,当\(\lim B \to A\)时,得到的“极限L线”不一致,所以原点、也就是A点处的切线是不存在的。
但是上面这个答案、或者说解释,以我现在的数学水平,是无法“透彻理解”的。原因在于:
1、我为什么不能说这一点上有2条切线?为什么偏偏要说这一点上的切线不存在?难道图像上任何一点只能最多只有一条切线吗?
2、\(\lim B \to A\)并不是\(B = A\),而直线既然是通过A和B两点定义的,那么在\(\lim B \to A\)时就不是严格的\(B = A\),此时通过极限得到的\(L_{limit}\)与\(B = A\)时得到的\(L_{B=A}\)就一定是一样的吗?这里额外的又回到了上面的问题:\(L_{B=A}\)没有2个点,怎么定义出的直线呢?
不想了,想多了脑袋痛。我觉得想通过“极限”定义出切线,也许还有其他基础知识需要学习。换句话说,我隐约感觉:或者是我的学习脉络不正确;或者是这个定义的脉络不正确。也许应该先有导数的定义,有了导数的定义就有了斜率的概念、有了斜率和点A,就可以通过直线的另一个定义方式——点斜式——定义出直线。
所以如果按“将定义脉络翻过来”的想法来解释,也许就是:图像上某一点要先可导,当它可导时就是有斜率的,从而通过“点斜式直线定义”,这一点就是有一条“点斜式可唯一定义出的直线”的,从而这样一条唯一存在的直线就是该点的“切线”。
二、额外的问题:
在搜索上面的问题及尝试通过互联网找到答案时,看到网上有这么3句话:
1、在数学中,切线是与曲线在某一点相切的直线。更严格地说,曲线上某一点的切线是该点处的最佳线性逼近。切线的定义依赖于“可微性”的概念。如果曲线在某一点处是可微的,那么该点处的切线是唯一的;
2、如果曲线在某一点处不可微,则该点处的切线可能不存在,或者不唯一;
3、如果切线的斜率为无穷大,则切线是垂直的;
上面这三句话令我更加“头晕目眩”了。原本的问题没有得到解答,却又多出来更多的“读不懂且理解不了、想不出具体情形”的表述。我现在对数学学习的感觉就是:不要想太多,能把课后习题做出来,就知足了。