一、例题的出现

在《复变函数》最开始的部分，有一道例题，有如下两种表述方式：

例：证明：函数 \(f(z) = |z|^2\)在z=0点可导，且导数等于0。

或者另外一种表述方式：

例：讨论函数\(f(z) = |z|^2\)的可导性。

上面两种表述方式其实是一样的，针对的都是相同的函数\(f(z)\)，研究的课题也是一样的：求出它在\(z=0\)点的导数。有趣的是，这两个表述方式都巧妙地避开了“不严谨”。

如果让我出这道题，也许会被写成：计算出\(f(z)=|z|^2\)的导函数\(f'(z)\)，并求出\(f'(0)\)的值。

按照我的设问方式，实际上也是可以正常进行这道题的求解的，但是“问法”相当于已经默认了这个复变函数是“处处可导”的了。上面的例题使用的设问方式就很“狡猾”，它们知道这个函数并非处处可导、只在\(z=0\)时才可导，所以从最初的设问环节开始，就避开了“不严谨”的说法。

所以这道题按照例题的问法，至少应该从以下2个方面完成：

1、深刻的理解导数和导函数是什么，小心地求证原函数是否在指定的点处可导；

2、如果原函数并非处处可导，而只在部分区域上可求导。则要看题目要求的求导点是否在可导区间上（例如本例题要求在\(z=0\)点得出导数值），在可求导区域内则进行求导、不在可求导区域内则不存在对应的导数。

二、函数可导、导函数的意义

个人理解：函数可导、有导函数，大意似乎是：这个函数连续、并且拥有连续的渐变光滑性，其中连续的渐变光滑性的意思就是他在图像上的每一个点上都有切线存在。

上面的说法如果正确的话，在实函数上是可以比较方便的通过图像理解的。但是对于复变函数而言，图像上理解起来有一些吃力。我还不知道如何通过图像去理解这个事情（图1、图2）。

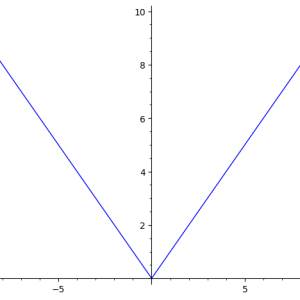
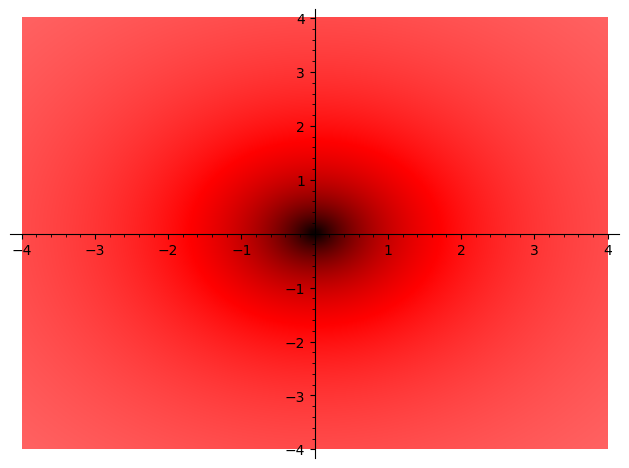
例如下图1，就是相关复变函数的图像，从这个图像上能看出函数的确是连续的、并且是渐变的，如果它的导函数也是连续的、渐变的（所有的色彩过度都是渐变衔接），那么这个函数就是有导函数的。但是从图2来看，这个函数的导函数并不是在每一个区域都是渐变的，它只在所有的横坐标上有着渐变色彩，而在任何一个纵坐标的垂直线上，都是“固定单色”，不在拥有色彩的渐变性。因而大概猜测，这个函数的导函数是不存在的。

图像1：函数\(f(z) = |z|^2\)的图像

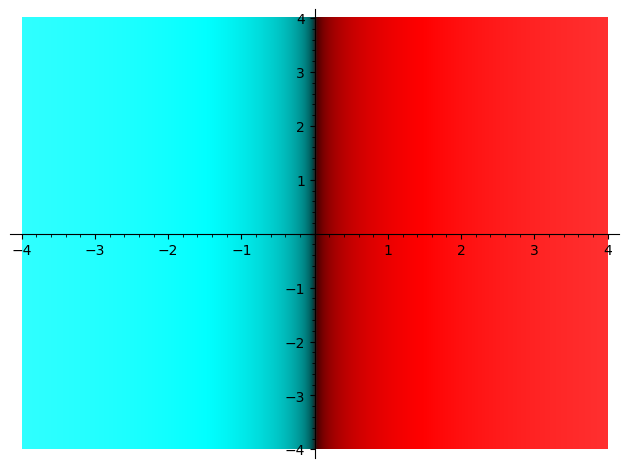
图像2：函数\(f'(z) = \frac{df(z)}{dz}\)的图像

三、除z=0点外，其他地方不可导

“深色教材”的P17页就是上面的例题，但是我还是没有完全理解。整体意思就是它最终得出的结论就是，在除了z=0的点以外的地方，导函数的值都不存在极限，因而也就不可导。具体的求证过程如下：

已知函数 \(f(z) = |z|^2 \)，此时，由导数定义可知 \(\lim_{\Delta z \to 0} \frac{f(z_0 + \Delta z) – f(z_0)}{\Delta z} = \lim_{\Delta z \to 0}(\overline{z_0} + \overline{\Delta z} + z_0 \frac{\overline{\Delta z}}{\Delta z})\)

情况1：当\(z_0 = 0\)时，上式很容易看出来是趋于0的，所以极限存在、且是0；

情况2：当\(z_0 \neq 0\)时，上式的极限将等于\(\overline z_0 + z_0 \frac{\overline {\Delta z}}{ \Delta z} \)。此时第二项中的“分数”是多少呢？这里就要再展开详细的推敲一下，也就是产生了一个新的子问题：

子问题：已知\(z_0 \neq 0\)，求\(\lim_{\Delta z \to 0} z_0 \frac{\overline{\Delta z}}{\Delta z} \)

五、当\(z_0 \neq 0\)时，求\(\lim_{\Delta z \to 0} z_0 \frac{\overline{\Delta z}}{\Delta z} \)

上面已经将问题转成了新的问题，现在对这个新的问题进行推导。书上这个过程是非常简略的，但是我数学基础差、脑子也不好使，所以展开一点点的推导。

对于上面的问题，原书上说了一句：令\(z_0 + \Delta z\)沿直线\( y – y_0 = k (x – x_0)\)趋于\(z_0\)。而我恰恰就是这句话不理解，好在最终想明白了。如果画个图，比较容易说明这个事情，但是一旦画图了，纵使不再去“说明”、也是“不言自明”的了。

还是“啰嗦”一些，从最基础的、画图的，来继续记录这段学习生涯：

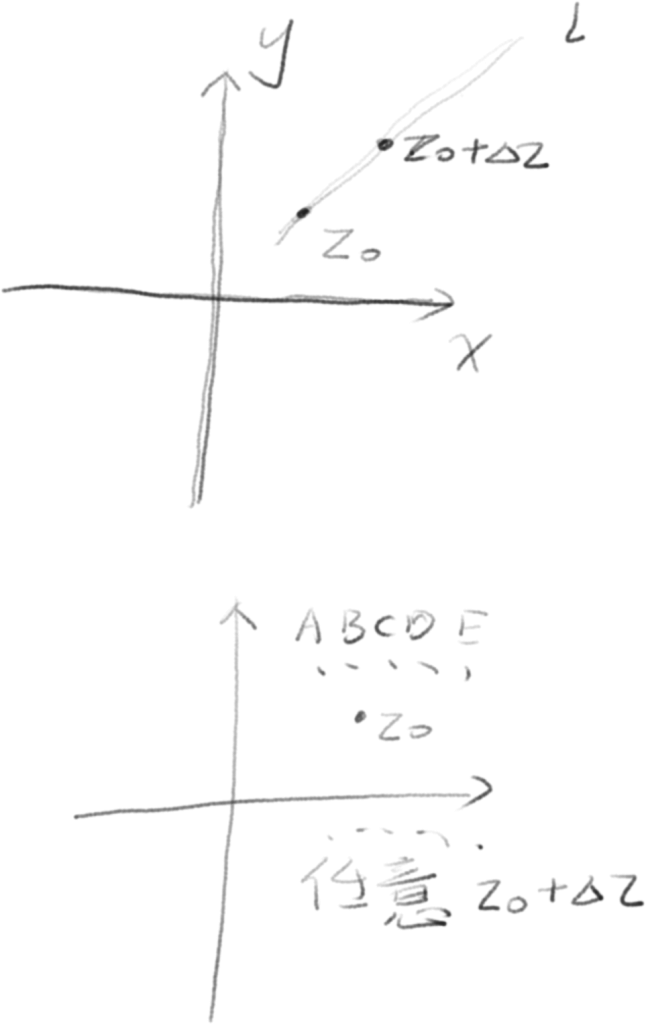
从上面的图1中可以看出来，\(z_0\) 和 \(z_0 + \Delta z\) 是两个点，这两个点的连线\( L \)有着一个斜率。同时再看上面的图2，会发现在\(z_0\)点周围，实际上是可以找到无数多个\(z_0 + \Delta z\)的，这里先将结论：斜率可以是任意的，记下来。

\(\lim_{\Delta z \to 0} z_0 \frac{\overline{\Delta z}}{\Delta z} \) = \(\lim_{\Delta z \to 0} z_0 \frac{\Delta x – i \Delta y}{\Delta x + i \Delta y} \) = \(\lim_{\Delta z \to 0} z_0 \frac{1 – i \frac{\Delta y}{\Delta x}}{1 + i \frac{\Delta y}{\Delta x}} \)

结合上面的图像，知道\( \frac {\Delta y}{\Delta x} = k \)，也就是：\(\lim_{\Delta z \to 0} z_0 \frac{1 – i \frac{\Delta y}{\Delta x}}{1 + i \frac{\Delta y}{\Delta x}} = \lim_{\Delta z \to 0} z_0 \frac{1 – i k}{1 + i k} = z_0 \frac{1 – i k}{1 + i k} \)，此时斜率k就是上面提到的，可以是任意的。

六、最后一个问题

所以上面的问题又一次衍生出了新的问题：当\(z_0 \neq 0, k \in R\)时，\(z_0 \frac{1-ik}{1+ik}\)等于多少？

这个问题对我而言“可能”比较简单了，所以直接说结论：结果是不定的。最后，因为这个计算式中k的任意性导致结果不确定，所以一路还原到最初的问题上，就得出了当\(z_0 \neq 0\)时，极限不存在，因而也就是原函数不可导。

注：这里说的“可能比较简单”其实也不简单，如果展开推敲，还是有很多基础知识的欠缺，但是虽然没有言之凿凿地定理（头脑中没有），但几乎都可以说是显而易见的结果不一定，所以也就不再过多的赘述了。

七、结论

这道例题的目的是说明如下事实：

1、函数可导处必然是连续的；

2、函数连续处，并不一定是可导的；

3、在实函数中，上面“可导处必连续、连续处不一定可导”的例子并不常见；

4、在复变函数中，上面“可导处必连续、连续处不一定可导”的例子非常常见、可以说是比比皆是。