一、基尔霍夫电压定律:
在《电容电压跟随电源电压的过程》中给出了电容电压跟随恒定电源电压的公式,但是没有进行具体的推导过程。这个推导过程在参考文章里面有、不过比较简略。在具体推导时,正负号、常数项等细节容易产生错误,所以我还是想比较详细的记录一下推导过程。
\sum V = 0首先根据基尔霍夫电压定律知道:沿着闭合回路所有器件两端的电势差(电压)的代数和等于零。也就是说:
\sum V = V_B + V_C + V_R = 0在这个电路中有电池、电容、电阻,它们3个电子元件构成了闭合回路,其中电池升压、电容降压、电阻降压。
V_C = -\frac{Q(t)}{C}电容的压降,因为是“压降”,所以取负数。
V_R = -I \times R电阻的压降,同样也是因为在电阻上电压也是“降压”,所以也是取负数。关于正负符号的选取,其实我现在还不是十分的肯定,只是因为参考文献中是这样写,所以就先“强行解释”,但具体的、本质的取负号原因,还要再进一步的推敲。
\sum V = V_B + V_C + V_R = V_B -\frac{Q(t)}{C} -I \times R = 0将以上3个公式合并之后,得到整个环路的基尔霍夫电压计算式。
I = \frac{dQ(t)}{dt}经过电阻的电流(也是整个电路中的电流)I,这里用到了微分式。这里其实还有一个细节问题,可能需要额外的一篇blog进一步的推敲(为什么电容电压直接用Q/C,而无需加上微分项)。
V_B -\frac{Q(t)}{C} – \frac{dQ(t)}{dt} \times R = 0再次带入,便得到了准备进行求解的方程,如上所示。
\frac{dQ(t)}{dt} = \frac{V_B}{R} – \frac{Q(t)}{R \times C}经过整理,可被整理成标准的微分方程形式。
此时可以看出来:
1、欲求解的就是Q(t)这个函数,它意味着随着时间t,电容器上积累的电荷量是多少,换言之,也就是随着时间t,电容器上的电压(Vc = Q/C)是多少;
2、虽然现在还没有解出Q(t),但也能看出来Q(t)的变化率是随着t的变化而变化的;
二、推导、求出Q(t)方程:
下面开始具体的求解推导。首先对上式进行变换,得到:
\frac{dQ(t)}{ Q(t) – V_B \times C} = – \frac{dt}{R \times C}将微分符号dQ(t)和dt分别放在等号的两边,这样便可以分别对左右两边进行积分。注意上面的公式中右边多出来一个负号,是因为在变换等式时,左边的分母中的两项位置进行了调换。之所以左边分母要进行前后项调换,目的是令左边在进行积分时是标准的ln积分式、以方便积分。
\int \frac{dQ(t)}{Q(t) – V_B \times C} = – \int \frac{dt}{R \times C}两边同时进行积分,左边是“ln积分”,右边是“幂积分”,都是简单形式的积分,可以直接得到结果。
ln | Q(t) – V_B \times C | = – \frac {t}{R \times C} + K因为两边都是不定积分,所以左、右都是有常数项的,将常量合并成1个、并暂定名K,放在等式右边。这里额外的还有一个困惑:为什么常数项要放在右边?如果将常数项K放在等式的左边,似乎会对最终的结果有影响?
答:上面的“困惑”是不存在的,详见《这篇文章》。
ln ( V_B \times C – Q(t) ) = – \frac {t}{R \times C} + K去掉绝对值符号:推敲一下绝对值符号内部,会发现:这个为电容充电的过程,是电源将电荷给予到电容器上,而电容器始终不会“吐出”电荷,所以电源电量始终大于(最终时刻等于)电容电荷量,所以去掉绝对值符号时,绝对值符号内部的减法项要颠倒一下,才能确保正确的符号取值。
ln ( V_B \times C – Q(0) ) = – \frac {0}{R \times C} + K求出常量K的值:带入初始条件,开始t=0时刻,电容内电量为0,即Q(0)=0。
K = ln (V_B \times C)求出常量K的值。
ln (V_B \times C – Q(t)) = – \frac {t}{R \times C} + ln (V_B \times C)将已求得的K值,带回Q(t)的方程中。如上得到一般方程。
ln (V_B \times C – Q(t)) – ln (V_B \times C) = – \frac {t}{R \times C}将ln表达式合并到等式左侧。
ln \frac{V_B \times C – Q(t) }{V_B \times C} = – \frac {t}{R \times C}ln表达式“外减”变换成“内除”(这里有没有更准确一些的数学表述呢?)。
e ^{ln \frac{V_B \times C – Q(t)}{V_B \times C}} = e ^ { – \frac {t}{R \times C}}等式两边同时“加底抽指”,目的是(这里缺少进一步的目的说明)
\frac{V_B \times C – Q(t)}{V_B \times C} = e ^ {\frac {-t}{R \times C}}等式左边化简、最终得到上面的公式。
最后,再将Q(t)孤立出来:
Q(t) = V_B \times C \times (1 – e^{\frac{-t}{R \times C}})如上得到最终的方程解。
V_C(t) = V_B \times (1 – e^{\frac{-t}{R \times C}})等式两边同时除以电容C,便可以得到电容电压Vc关于时间t的方程。
假设电源电压为12V,电容容值为1法拉,电阻假设为1000欧姆,带入上式并绘制图像:
V_B(t) = 12 V_C(t) = 12 \times (1 – e^{- \frac{t}{1000 \times 1}})plot(Vb, 0, 10000) + plot(Vc, 0, 10000)
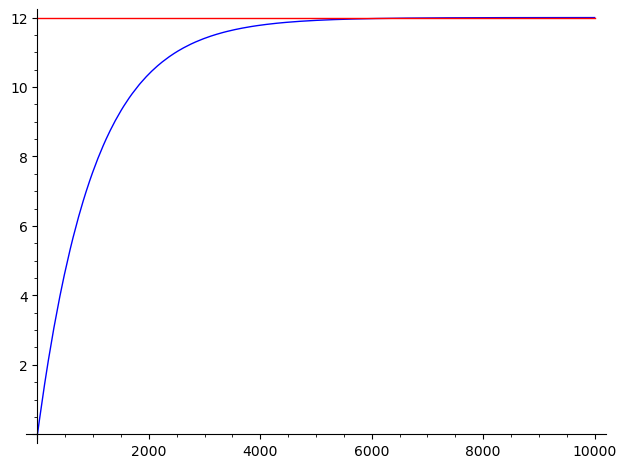
从图像中可以看到当电路闭合之后,电容会以很快的速度被充电,随着电容电势逐渐建立、并趋于电源电势时,充电逐渐缓慢下来,并且会愈发的逼近于电源电势。
在理想的情况下,电容电压只会无限的接近于电源电势,而不会抵达电源电势。但是在实际的现实情况下,因为环境的热扰动,电源并不会真的一直是12V稳定、持续的存在,电源的12V电压在各种环境热扰动下总会出现小的波动,这些小的波动足以令电容电压与电源电压产生交点,从而完成电容最终的充电。
另:最近再看有关量子力学的入门介绍,如果能量是量子态的,那么上面提到的“无限逼近”在更细分的尺度上就也不会是连续的,而是变成量子化的,那么即便没有热扰动,在足够的细分情况和足够的等待时间之后,电池向电容充电的最后时刻,也会因为能量的不连续而“一份份”的想电容供给最后的能量,使得在最终时刻、总有那么一个最终时刻,电容上的电压会从“无限逼近”通过一份“量子化能量”,“跳变”到与电源电压一致。
三、回路中的电流随时间t的变化关系:
因为电源电压始终是12V,而电容电压Vc(t)已经解出来了,此时电阻上的压降便可以求出来;
同时,电阻上的电压与电阻的比值是电流,而又根据闭合回路电流处处相等,可知电容上的电流等于电阻上的电流,电容上的电流可以用电容电流计算式得到,所以有如下等式成立:
I_R = I_C再进一步的考虑:
I_R = \frac{V_R}{R} = \frac{(V_B-V_C)}{R} I_C = \frac{dQ(t)}{dt}综合上面3个等式,可以得到如下的等式:
\frac{(V_B-V_C)}{R} = \frac{dQ(t)}{dt}上面的等式的成立性证明暂时先不证明了。只先完成电流关系式的确定。也就是进行微分计算:
\frac{dQ(t)}{dt} = \frac{d}{dt} (V_B \times C \times (1-e^{\frac{-t}{R \times C}})) = V_B \times C \times \frac{d}{dt} (1-e^{\frac{-t}{R \times C}}) = I(t) = \frac{V_B}{R} \times e^{\frac{-t}{R \times C}}最后,依然以电阻R=1000Ω、电容C=1F、电源电压为12V进行绘图,得到电路中的电流图像:
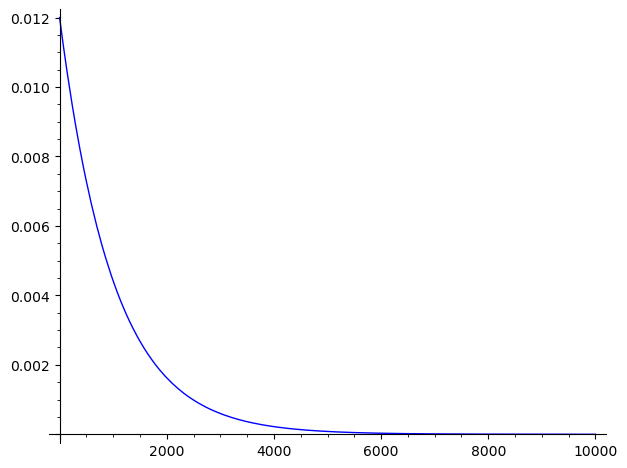
可以看出这个电路中,初始电流是最大的,这是显然的——因为电容起初是“空的”,会以最快的速度吞噬能量。随着电容内电荷的聚集,电路中的电流会逐渐减小,待电容被充满电之后,电路中将不在有电流通过。
在直流电路中,电容充电阶段会产生电流,在电容满电之后就相当于“断路”不再有电流。从而说明了电容“隔直通交”中的“隔直”过程的形成过程。