一、问题的提出
在上一篇博客《电容电压跟随电源电压的过程》中,基本搞清楚了电容的充电过程和放电过程电压的变化规律。但是它对我想了解的电路而言太基础了,根本无法指导我对当前电路的分析。
我更想搞清楚的是当电源为交流电时,电容电压的跟随情况,如下图所示:
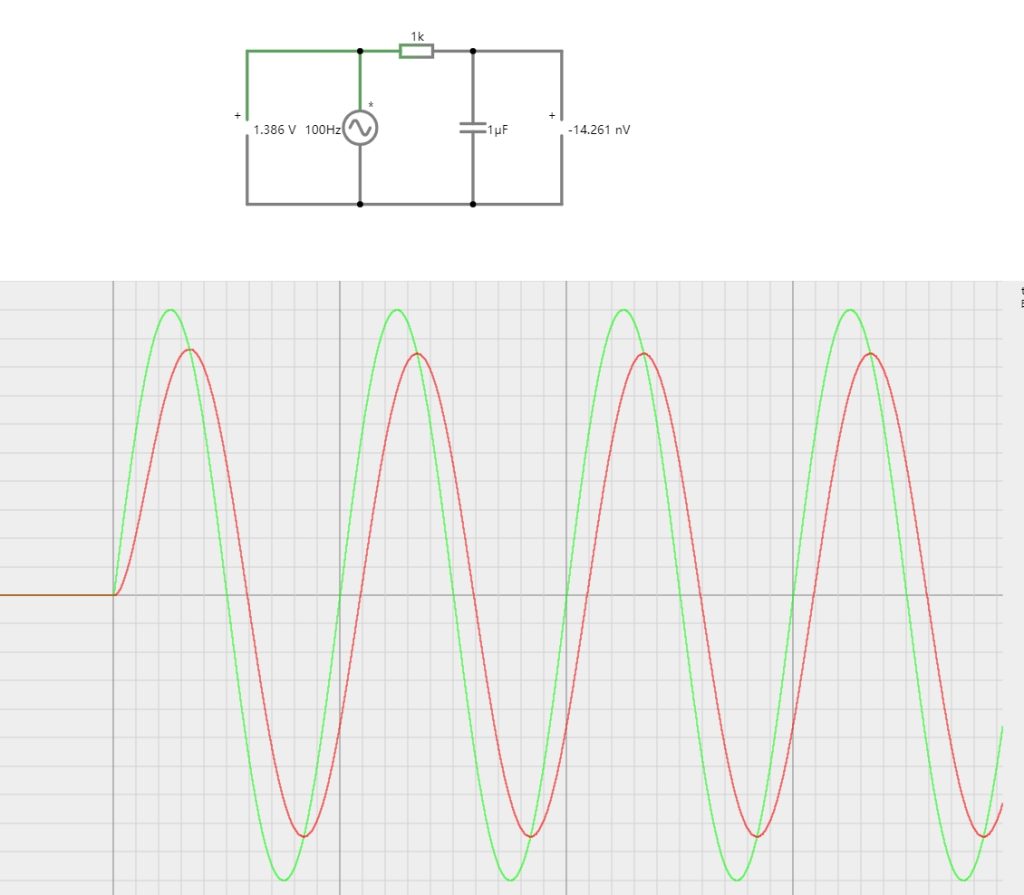
图中的电源是100Hz的5V交流电,可以看到在电容上形成的电压的峰值(红线)略微低于5V,并且是滞后于电源电压的。这在网上已经有不少公式说明了它们之间的关系,但是却没有给出推导过程。
并且更为令我不安的,是这些现成的公式都是指电路进入“稳态”之后,而在上电的起始阶段,可以看出电容与电源之间的电压并不出现相位差。
所以在我想来,这个“现成的公式”是无法解答我的困惑的,所以这篇文章以及接下来的一段日子,我将尽可能搞清这个问题:电容电压是如何跟随交流电压的。
二、困扰
又陷入了“AI胡说”的困扰,这篇博客提出来的问题,我自认为问题定义的还是比较清晰的,但却找不到准确的文献。如果继续执着于利用搜索引擎或AI问答引擎,恐怕接下来要浪费的时间将是巨大的。
其实我觉得这个问题应该比较容易,它只是在解如下的方程:
\(\sum V(t) = U_{S}(t) + U_{C}(t) + U_{R}(t) = 0\)这似乎没什么难度,但因为缺少相关的参考资料,所以我很难确定自己的推导过程每一步是否准确。尤其又因为我自己解出的答案,绘制成图形之后和预期的图形相差太远——因而可以确定我的求解是错误的。
有些不知该如何继续了。
三、找到了正确的计算公式、虽然并不完美
经过多次的搜索、查找,终于找到了一篇“正确的”参考资料:
https://www.iitp.ac.in/~siva/2016/ee101/Sinusoidal_Steady_State_Analysis.pdf
之所以可以认为这篇参考资料是正确的,是因为基于这篇资料计算电容电压,绘制出来的电容电压的波形是准确的(相移角准确、电容可以得到的最大电压准确、并且是稳定持续输出的):
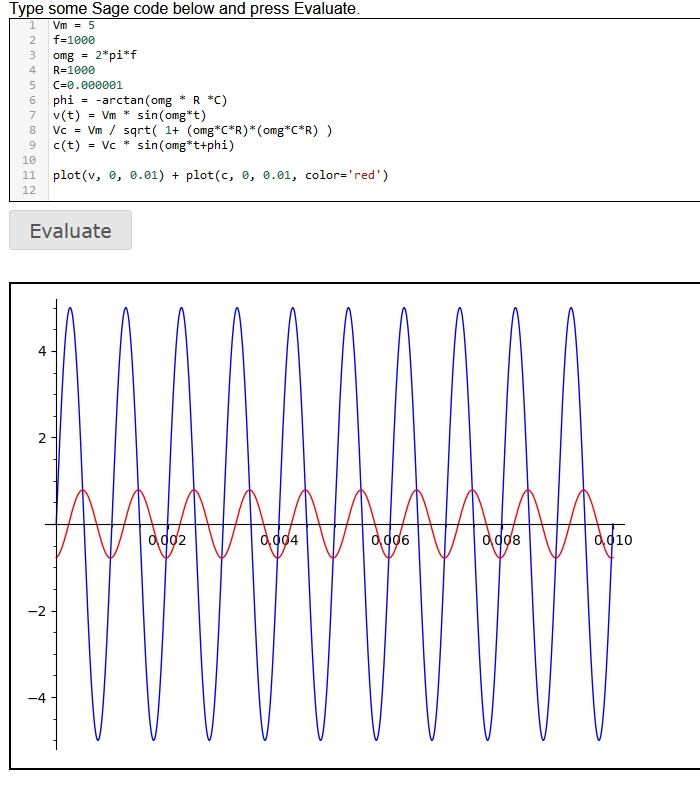
这很不容易!我之前一个下午都在使用AI问答引擎找答案,结果给出来的各个计算公式都不正确。直到晚饭之后,都已经准备放弃了。但不甘心又找了一下,才找到上面这篇文档。
虽然这个文档给出的结论并不是我要的最终结论——它显然缺少系统上电的起始阶段的分析和曲线。但至少有了稳态之后的正确公式,可以先把后面的知识了解、掌握一下。
四、瞬态响应阶段和稳态阶段的完美波形
我感觉自己是找到“宝”了,上面的参考文档实际上是准确、完美的。只不过起初找到的时候没有细看,草草的照葫芦画瓢画了个初步的图形。细看之下,这篇文档实际上是含有初始瞬态响应阶段的分析的。按照最终的正确公式进行绘图,得到的图形正确、完美:
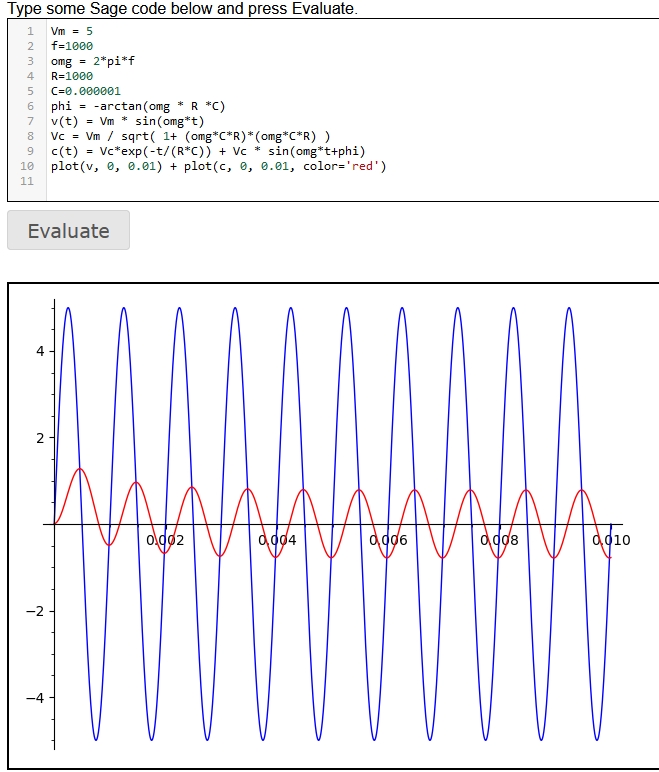
文档中给出来的推导公式也非常的简要明了。所以接下来只需要将文档中提及的公式好好学习、自行推导一遍,这一目的功课就应该算是完成了。
五、小节
1、其实上面的图形我完全可以在仿真软件里模拟出来,然后直接截屏就可以正常使用了。但是之所以纠结这个图形的产生过程,是因为我想搞清楚仿真软件中这个“电容电压跟随电源电压”的计算过程,究竟是怎样的;
2、如果不知道具体计算过程、不知道具体的推导过程,就很难理解为什么最终是RC的阻值、容值决定了它的相移。也无法自己利用SageMath绘制图形。不能自己绘制图形,就很难在博客文章或者“视频文章”中给出更详细的展现;
3、如今已经有了这个具体的“绘图公式”,我就可以按照自己之前的想法,绘制一系列的曲线,通过这些曲线说明为什么每一个RC网络可以实现(0°-90°)之间的相移、为什么必须需要至少3组RC网络才能形成180°的相移;
4、额外的,除了可以说明三组RC网络形成的180°相移外,还可以计算出最终反馈回去的电压有多少,与控制极的初始电压叠加之后形成的控制极电压波动有多大、进而推算出控制极的电流形成的开关效应,最终将Jack Kilby的RC Phase Shift Oscillator解释清楚了。