一、问题的提出:
一颗有电且“满电”的电池,它的正极有着比负极更高的电势。
当将这颗“满电电池”的正负极通过导线连通时,通过电场力的作用,这条通路上的电子便会从低电势区域向高电势区域移动,目的是减小正负极之间的电势差,从而形成电子持续的定向移动,也就是电流。
因为这条导线是理想的、电池也是理想没有内阻的,所以电子的定向移动不会受到任何的阻碍,单位时间内通过导线横截面的电子数量可以无限多、电流无限大,只需近乎于0秒的时间,电池正负极的电势差就被拉成零、没有了电势差。
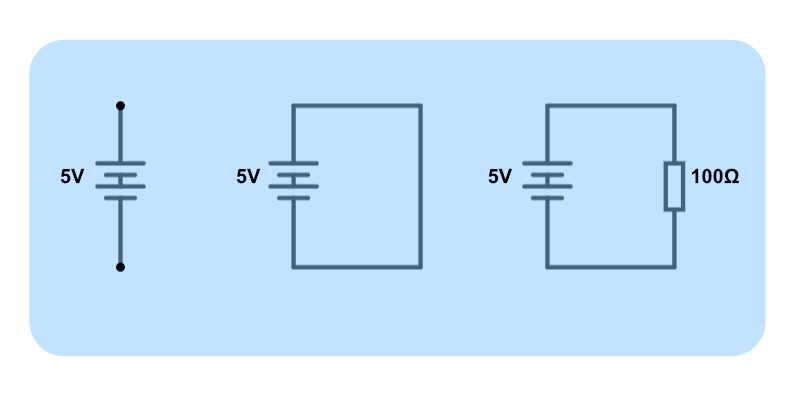
重新回到初始状态,在这条理想导线上加入一颗电阻,目的是阻碍电流的移动,使得导线上的电流不再是无限大,而是I=U/R,问:此种状态下,需要经过多少时间,电池的正负极电势差才能从U降低到0呢?
二、初步讨论
上面的问题中,一直用的是“电池”,目的是让问题更感性一些。其实这篇文章主要聊的是电容,因为电池和电容基本相似、可以类比,所以上面一直用“电池”来做表述。但电池和电容本质上是有差异的,所以为了更加严谨一些,下面不再使用“电池”的称呼,而是用“电容”来继续讨论。
一旦系统接通,电池(电容)将开始进行放电,电流经过电阻做工,并且逐渐的电容内部的电压会降低、直至电容电压降低到0。这也是上面提出来的问题:要经过多久的时间,电容电压才会从初始电压(例如5V),降低到0V呢?这里有一个值得注意的事情:电容初始电压虽然是5V、在系统导通的起始时刻,流经电阻(100Ω)的电流是I=5V/100Ω=50mA,但是这个电流并非恒定不变的。
随着时间的推移,电容内部的电场强度(如果是电池、则可以理解成电量)会越来越低、电容的端电压也会随之下降,从而导致流经电阻的电流也会越来越小。这个过程是连续的——每一个当前时刻的电流都是上一个时刻的电容电压决定的。在没有仔细的推敲之前,不妨先随手胡乱的画一画它们随时间t的变化关系:
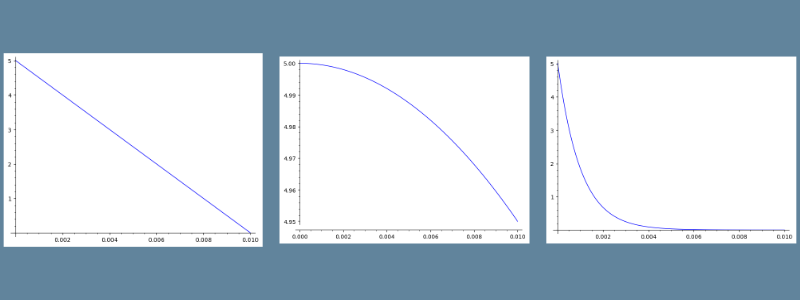
如上的若干图形都是肆意画出来的,只有大概的猜测、并没有任何的理论依据。大方向上而言,电容电压随时间的推移一定是越来越低的,但究竟是上面图中哪一种形式呢?如果花更多一些时间思考,似乎能从“电能密度”的角度上猜测出,上面的3个曲线中,最右边的曲线似乎是更贴近于真实情况的。但也只是猜测。
另外,我们最关心的“经过了多长时间,电容电压变为0”,在上面的图形中也是无法推敲出来的。虽然我们知道这个时间一定非常小,所以图中都是“拍着脑袋决定”,在0.01s的时候,电容电压就已经降低到0V了,但实际情况究竟应该是怎样一个时刻?所以接下来就要从数学的角度具体推算一下了。
三、具体数学推导
电容放电过程中的电压变化,可以从两个维度上考虑,分别是KVL和KCL两个角度,也就是考虑电容上的电压时时刻刻等于电阻上的电压、或电容上流出的电流时时刻刻等于电阻上流过的电流。这两种思考角度本质上是一样的,具体的推到过程由下面的两个参考资料中可以详尽的看明白:
1、以电压考虑,依据Kirchhoff’s voltage law (KVL)进行推导:
参考资料:https://web.mit.edu/sahughes/www/8.022/lec09.pdf
2、以电流考虑,依据Kirchhoff’s current law (KCL)进行推导:
参考资料:https://mechatrofice.com/circuits/charging-capacitor-derivation
3、额外的,一篇不错的科普概述文章:
这里直接给出最终的结论,电容上的电压随时间T的关系式是:
\(V_{C}(t) = V_{0} \times (1-e^{-\frac{t}{RC}})\)由此看出电容电压在数学上是永远不会等于0的,它只会越来越趋近于0。但是现实世界中,因为电路上的IC并非理想的、并且存在着热扰动,所以只要经过一段时间,电容趋近于0的电压就会因为一个“小的波动”而抵达X轴,从而时电压归零。
update 2024.06.06:上面的电容电压随时间t的方程,我自己推导了一遍,这样对理解这个过程还是有一定帮助的。具体推导过程见《电容跟随电压过程公式推导(1)》。
四、后记
1、写此篇博客的目的和智能问答AI:
写这篇博客目的是熟悉一下各个辅助工具(例如SageMath、LaTex、LTspice等)的使用方法,以便后面的博客写作更加熟练。
借助于当下流行的人工AI问答工具,节省了大量的搜索和推算时间。人工AI问答工具是把“双刃剑”,它的回答正确时的确可以方便的找到答案,主要是在不会提问的时候,可以通过几次提问,令自己逐渐找到提问的方式、方向,并且让自己知道应该问什么词语。
但是对于AI给出的答案,则是“五花八门”,甚至于有些时候它就是信口开河,可谓是一本正经的胡说八道。明明是错误的推导,也被AI说的有模有样,十分迷惑人。这个时候就是最浪费时间的,思路被它带偏不说,还会花大量的时间以为是自己的问题。
2、电容的充放电过程:
本文暂且指整理出了电容的放电过程,对于充电并没有讨论。但是只要对放电过程的数学公式有了清晰的了解,充电过程也就可以容易的理解并掌握了。
3、直流电压下电容电压的跟随:
本文讨论的是电容自己做为“电源”对外放电。但实际上我更关心的是系统内有一个直流电源,而电容视为“被充电”元件时,电容的电压表现。所以虽然说过程相反、原理相似,也容易理解,但还是要再花时间另开一篇博客学习、整理。
4、交流电压下电容电压的跟随:
之所以要完成“在直流电压下电容的充电过程”的学习,是因为我最终的目的是学习、掌握当电源是“正弦交流电”时,电容的电压同电源电压的跟随情形。所以这里也是一个知识点的欠缺。并且现在感觉,这个问题将会更加复杂一些,尤其是在数学推导上,也许存在着更高深的数学知识,需要从基础学起。
5、最终目的:
只有在完成了上面提到的电容电压随交流电源跟随的情况,会计算、会画图之后。才能将RC Phase Oscillator振荡器中,为什么会有3组RC相移网络的事情搞清楚、说明白,所以这篇文章实际上只是之前学习Jack Kilby的RC相移振荡器的基础中的基础。