试使用SageMath进行函数图像的绘制。例如：对于复变函数 \(f(z) = cos(-2 \alpha ) + isin(-2 \alpha )\)
上面函数，可以使用SageMath绘制出在复平面上的图像：
sage: f(z) = cos(-2arg(z)) + Isin(-2*arg(z))
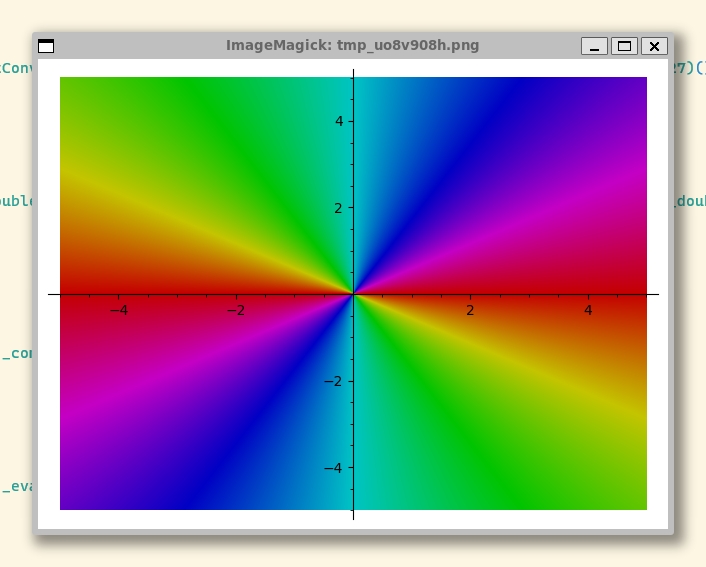
sage: complex_plot(f, (-5,5), (-5,5), plot_points=50)其中的complex_plot()和plot()相似，只是声明为在复平面上进行绘图。后面的第一个(-5,5)指实坐标范围从-5到+5，第二个(-5,5)指的是虚数坐标、也就是复平面上的纵坐标、从-5i到+5i。
绘制出来的图像比较“抽象”，大概能看出来是通过彩色的衔接来表达是否连续，但这五颜六色的色彩对我而言还是比较陌生、一时难以理解的。
生成的图像是：
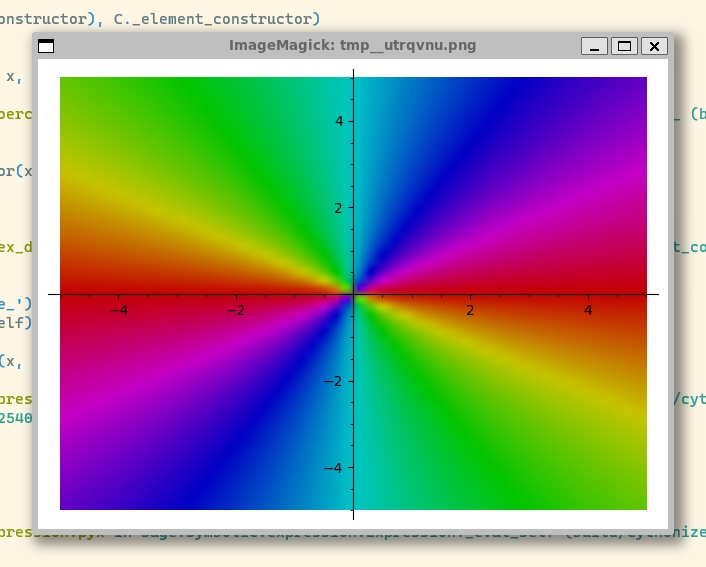
上面的图象太模糊了，改变参数，调整为plot_points=500，可以得到更清晰、精致的图像：
小程序開發已經用三脚貓功夫做了一些粗略的實現，接下來就是學習這個技術框架中的細節，并且返工之前粗略、粗糙的地方。今天學習了一下幾個技術技巧： 一、子控件向父控件發送帶參數事件消息 頁面上的button按鈕是我做的一個子控件、這個按鈕是放在panel控件中的。現在我想點擊button按鈕的時候，button按鈕完成響應、并將事件通知給panel，由panel接收並繼續處理事件。 此前的實現非常拙劣，就是只使用panel進行事件的處理： 這樣做的壞處是顯然的：觸摸會發生在整個panel中。而我希望的是觸摸僅由裏面的button受理。改造過程如下： 1、首先panel的頁面層，調整代碼如下： 這樣調整之後，panel不再接受bind:tap消息，而是會接收名爲customEvent的事件，一旦接收到customEvent事件，則進行running執行。此時的customEvent事件將由button發出，所以button的代碼寫成下面的形式： 這樣只要點擊了button，就會運行sendEvent方法，這個方法内實現向父層發出消息的過程，具體js代碼是： 通過triggerEvent發出了一個customEvent事件，父控件因爲綁定了這個事件、接收到並開始處理就可以了。 二、動態成員訪問的方法 類似如下的PHP代碼： 在JavaScript中的實現方式是： 三、控件數據初始化 微信小程序的components控件，似乎沒有（我不確定）如pages頁面那樣的onLoad()方法，儅加載了一個小控件之後，向這個控件中傳入一些初始變量，便沒有辦法找到一個Init()或onLoad()的地方，對這些傳進來的變量進行預處理、以被在頁面上使用。 此時可以使用控件的observers監聽服務，對傳遞進來的變量進行監控，一旦傳遞進來的變量生效，observers服務啓動，以便進行數據的預處理操作。具體代碼如下： 四、頁面中的if/else流控方式 此前頁面中一直是這麽寫： 現在有了更好的方法： 雖然在頁面上的if/else流控寫法我已經瞭解了，但感覺并不如C/C++那樣直觀，總感覺有些奇怪，擔心它的嵌套不準確。不過也不重要，總之今天掌握的，就是這些。
每年最闷热的日子到了，这段日子称为“三伏天儿”，“伏”大概是“藏”的意思，指的是地表阴气因为骄阳而隐藏到地表以下。整个地表都被烈日烘烤得阳气十足、再无阴凉。 也有人喜欢用“桑拿天”称呼这段日子，因为城市人不再做农事、可却喜欢泡“桑拿”，因而对他们来说，“桑拿”是个更形象的词汇、是随着新生事物诞生的新词。这个词来源于芬兰，芬兰语中的浴室或浴池称为“sauna”。 说起来估计在芬兰，人们去sauna也顶多就是冲冲水、洗洗澡吧。可城里人并不满足这样简单的洗浴形式，他们找到了更有妙趣的洗浴方式——蒸汽浴，同时再配上一个芬兰词，看上去更加的高大上、又有舶来味道。 坐在高温蒸汽房间中，借着热气腾腾的水汽将皮肤慢慢沁润、烘开汗腺，好似能够洗的更彻底、更干净、更通透、更过瘾。当然结账的时候花销也会更大一些。可是对于喜欢沉浸在体验中的城市人，这笔钱花的值得。只要体验好、感觉妙，花钱就是理所应当且无需吝啬的。 但若是让你在烈日的烘烤、高温的环抱中“享受一次免费桑拿”，恐怕很少有人乐意，哪怕免费也不会有人觉得这是享受。这着实是种煎熬。浑身不住的出汗，脖子上的汗渍反复被蒸干，从汗液中析出的盐分附着在因烈日灼伤的皮肤表面，瘙痒疼痛。 千万不要用手去抓，已经灼伤的皮肤经不住这样的力道，只会越抓越痒、如果忍受不住瘙痒而尽管解痒、解气的去抓挠，皮肤会被指甲划伤、进而瘙痒转成疼痛。这样的话即便是晚上回到家中，汗水已经洗净，白天抓过的地方依然又痒又痛、甚至红肿热辣，辗转在床上难以入睡。 所以三伏天，任谁都不大想出门免费蒸场桑拿，除非迫不得已。明智的人都会躲在房间中、最好躲在空调房中，享受着清凉，如果能再吃上一口冰镇西瓜，那才叫一个享受呢。 我便闷热的房间中苦苦煎熬，我的房间中并没有空调，仅有的风扇吹出来的都是35摄氏度的热气。不敢开窗、因为窗外吹进来的只会是更高温的热浪。只有不住的喝水、再偶尔将水拍打在头发上，三不五时的看看窗外，期待着一场雨水到来。 我在这间闷热的房间中，无所事事的 “忙碌”着手中的“电脑工作”。 这句话有些矛盾是吧？既然是无所事事、为什么要说是忙碌呢？这句话还有一些空洞无物，究竟什么是“电脑工作”？能够说出这种既矛盾又空洞的话，显然是因为我想自欺欺人。我没有任何的工作，但又不想承认自己闲着，所以就不断地在电脑上写字，写这篇文字，目的是让自己看上去似乎是个“作家”，我可没偷闲，我在创作呢。
这一章很简短，只有2个话题：如何进行隐函数求导、隐函数求导能够完成相关变化率的求解。这两个话题看的我是“一头雾水”，全都能够看懂、给出的例题也都会做，但其中的细节是没有一点儿能搞清楚的，总结就是这一章看的是“似懂非懂”。 一、隐函数求导： 1、什么是隐函数？这就是摆在我面前的第一个困惑，《普》几乎是很快就引入了隐函数求导的方法，而没有说明什么是“隐函数”，它是否是个更基础的、无需多说的知识呢？不得而知； 2、隐函数求导的具体过程。这一点对应着书中的§8.1，不费力气就看明白了。我在阅读这个章节的时候，对“链式求导法则”有了更豁然的理解，这个“豁然”要趁着现在还没有忘记、尽快花时间详细记录一下。否则一旦过段时间，很可能又会忘记掉； 3、具体的隐函数求导例题。没有什么难度，书中给出的例题都能跟着做出来。但诚如上面提到的，因为我不知道什么是“隐函数”，所以例题能做出来是没有意义的，原因在于：如果放在陌生的问题中，我可能很难一眼看出“这是一个隐函数”、“这里应该用隐函数求导去解决问题”； 4、隐函数求二阶导。同样的也可以将例题做出来，但是这里也存在着一个问题：我不理解二阶导的微分符号中，它的“分子”和“分母”中的上标位置区别的具体含义，或者说二阶导的上标符号具体是什么含义我不清楚。虽然能够隐约感觉到答案，但并不明确，所以这里也要再额外花时间推敲一下，形如下面的二阶导微分公式中，上标“2”的位置和具体含义： 二、相关变化率 1、§8.2章节是《相关变化率》的现实应用，以及利用隐函数求导方法求解。能知道说的是什么事情、能完成书中的例题的求解。 2、但是这些例题我自己却不会构建。不会自己构建例题说明自己完全不理解什么是“相关变化率”，不会自己构建例题意味着现实中即便遇到了“相关变化率”的问题或现象，也很难认识他们，知道他们，看得清他们，联想到使用隐函数求导的方式去解决他们； 3、相关变化率的具体概念要再花时间了解、学习。直到自己能够构建出例题、不费力气的就能信口举出例子、自己能够构建出应用场景和应用例题，才算是了解了这个话题。我现在能想到的比较感性的生活场景是人的吃饭、排泄，以及与体重的关系。这样一个生动的例子，如果能够随心所欲的构建出各类例子，并通过隐函数求导解决，应该就算是了解了。 三、小结 1、如上，就是这一章节的学习心得。可见这一章当前只是囫囵吞枣地阅读了、了解了，并不理解； 2、接下来将继续阅读第九章：指数函数和对数函数。
从网上看到的，试着做了做，没有做出来。所以记录在这里，等以后有时间了再重新尝试。 这道题我用绘图工具重新绘制了一遍题目，用的绘图工具是一个web工具，地址如下： https://www.geogebra.org
一、前六章学习小结 已经将第六章看完了，现在开始阅读第7章的内容。前六章的内容实际上讲解的非常缓慢，都是在介绍什么是极限、什么是导数、什么是微分。我阅读、理解的更慢，断断续续好几个月才看完。却至今还是没有十分明白。 什么是极限？ 极限是指某一个函数如，当自变量趋近于某一个定点时，这个函数的结果、也就是因变量将会趋近于的结果。极限是一个明确的结果、是一个明确的数值、是一个明确的“结果数值”。 什么是导数？ 导数和上面的极限不同，相对于“极限”而言，导数并不是一个明确的结果数值，而是因变量的变化量与自变量的变化量的比值，也就是当在某一个明确的点（如）上时，的比值。所以它是“比值”、而非“数值”。 什么是微分？ 微分是我仍然不理解的概念，上学时不理解、如今重学微分课程还是不理解。微分似乎既不像是上面的数值、也不像是上面的比值，微分什么都不是，微分只是一个“求导的过程”、“求导的方法”、“求导的思想”。微分是一种“细分思想”，利用这种“细分思想”或“微分思想”完成求导的思维方式。 同时，微分还是一个“符号”，使用“导数符号”表示的是比值结果，使用微分符号表现的是求出”比值“之前的”心路历程“。而且使用微分符号因为能够更多的展现出”求导的心路历程和动机目的“，所以在更复杂的求导过程中，利用微分符号可以更明确的将计算细节展现出来，进而使用各种”微分技巧“进行化简、转换、运算，以完成最终的求导、得到想要得出的比值来。 大概就是上面这个印象。也许还要再多花一些时间继续学习，才能有更透彻的理解。 二、额外的与模电联想 在模电中也经常会提到“微分电路”和“积分电路”，这里的两个名词具体含义也整理一下，也许过几天会用到。 微分电路：电路的输出信号与输入信号的导数成正比。换言之，微分电路输出的是输入信号的变化率。 积分电路：输出信号与输入信号的积分成正比。换言之，积分电路输出的是输入信号的累计值。 三、开始学习第七章的内容 接下来的第7章还是进一步对极限、导数、微分进行更多的例题讲解。只不过其中的例题都不再是多项式函数，而是三角函数。 大概翻看了一下后面的章节目录，后面的不同章节中，仍然是对极限、导数、微分进行更多的例题讲解，和第7章的大概方向是一样的，唯有不同的是，后面章节分别再对指数函数、对数函数、双曲函数……等进行求导、微分。 之所以简单的“极限、导数、微分”要如此一轮又一轮的重复，我猜也许是有如下2个原因： 1、不同的函数类型，微分思想虽然都是一样的，但用到的技巧各不相同，所以要区分讲解，从而不断地引入各种新的微分技巧或定理； 2、不同的工科应用领域中，用到的函数不同，例如在计算机行业中，也许就会经常用到三角函数、但很少用到双曲函数，所以不同专业的人可以有取舍的仅对自己行业频繁用到的函数类型进行微分思想练习。 如上是当前的学习小结。
数学很差、差到高中数学都已经忘光、总要借助网络或计算器才能得到答案。最近读《普林斯顿微积分读本》，想提升一下自己的基础数学水平，并争取从头到尾将这本书读完。 断断续续看了两个多月，才刚看到§6.6。接下来将继续阅读§6.7-直接画出导函数的图像。 这篇文章目的是做一个之前阅读的备忘，否则过不了几天，也许又是狗熊掰棒子——把前面已经阅读过的内容忘记了。 一、前面章节主要讲的是什么？ 主要讲的应该都是高中的数学知识，属于从高中的代数、向着高等数学微积分入门课程的过渡，这个承上启下的“衔接部分”，主要讲了极限、导数的概念，并且通过一些例题解释了如何计算极限和导数。 在介绍导数的基本概念时，大概讲了讲导数的本质——在图像上某一点的导数，就是这一点上的斜线斜率，换言之就是这一点上的最佳线性逼近。 二、我现在还不理解的事情有哪些？ 主要是今天在阅读的时候，在“速度和加速度”章节上的“加速度为负数”例题上，有一个知识点不会：求解，或者说对于形如的方程如何求解。 书中只说用“因式分解”可以得到两个实根，并且其中一个是负数在例题的环境下应该舍弃。并没有具体的推导过程，显然是因为一元二次方程求解属于高中数学知识，显然便不展开了。但我已经忘光了，所以不会求解。只好用最笨的方法——观察法，找到了它的解。（幸好这个方程可以通过观察找出解来）。 update 2024.07.04：经过重温一元二次方程求解方法，大概知道了配方法和韦达定理，并且已经用配方法和它推导出的最终直接求根公式，完成了这部分的例题。 三、接下去要继续学习 以上就是最近的读书笔记，接下去，继续看：§6.7-直接画出导函数的图像。