RC振荡电路初学笔记(1)
振荡电路(Oscillator Circuit)是用于产生特定频率和振幅的正弦波形或非正弦波形的电路。整句话有些拗口,简单来说:震荡电路就是可以产生正弦波形的电路。想要构成振荡电路,需要由三个基本功能单元共同构成:振荡器、放大器、反馈器。 比较常见的是LC振荡电路和RC振荡电路,因为最近在看《半导体发展史话》,其中提到了人类历史上第一枚集成电路芯片,顺着这个话题看下去,Jack·Kilby先生最初制造的三个基础电路之一,便是RC震荡电路。于是对RC振荡电路产生了兴趣,希望能够深入的了解一下。 RC振荡电路的组成方式比较多,其中使用元件数量最少、原理相对最简单的是RC相移振荡电路,即RC Phase Shift Oscillator Circuit,它仅需少量的RC网络、以及一颗开关管,即可实现稳定的震荡输出。 例如以下电路,仅需使用电阻和电容构成的RC相移网络(3组),在9V直流电压源驱动下,便可以产生固定频率的振荡输出(正弦波输出): 上图是比较常见的RC Phase Shift Oscillator电路,使用的是NPN开关管,但是Jack·Kilby当初设计的时候使用的是PNP开关管,这其中的差异和原因暂时并不重要,无论使用NPN还是PNP,先将基本的电路画出来、有个感性的认知便可以了。 Jack Kilby的发明所刊发的论文是 US3138743A,在其中提到了使用集成电路半导体生产工艺制作的几个电路图。在这篇论文所提及的几个应用电路中,最简单、最具代表性的便是RC振荡器。 但是这份发明专利看上去有一些吃力,主要是其中的电路图并不是我们今天熟悉的绘制方法。虽然图8.b和图8.c仔细看还是能够看出原理图的线框,但其中的符号对于初学者而言却有一些陌生,看似认识、其实与标准画法都有一些差异,它对相关电路的画法如下: 将上面的原文8.c重新绘制一下,大概是下面这个样子。这个RC振荡电路和今天比较成熟的振荡电路有一些差异,例如和本文上面所画不同,在 Jack Kilby 的论文中使用的是 PNP 开关管、而如今主流的则多是使用 NPN,或者在今天更多的则是使用 MOS 管、或直接使用放大器作为核心放大部分。 不过具体使用什么核心器件进行放大,本质上都是相似的。我想只要对其中一个细致深入的学习明白,其他的相似电路也就能够较快掌握了。所以接下来,我将对这个电路进行更详细的研究、学习。
UP4000焊接USB Type-B端子接口备忘
最近工作中用到了一台UP4000的小电脑,要从这台单板电脑(SBC)的主板上引出一个USB接口,与其他外部设备连接。 在UP4000的主板上,是有这个扩展设计的,它的CN15接口就是USB/UART扩展,这个CN15接口共有10个接线端子,其中可以引出2路USB总线。我使用的就是其中一路,也就是只使用这个接口的pin1-pin4引脚就可以了。 USB端子使用的是Type-B公口端子,线序定义网上也很容易找到。按理说从CN15到Type-B只有4条线,且这4条线的定义明确,应该很容易就搞定。但是我先后做过2批次的手动焊接,每一次都要再重新逐一核对这些线序的对应关系。想着也许今后还要再做这个工作,到时候可能又会忘记,还要再逐一核对,实在是太麻烦了。 所以干脆把这个工作做成图文,备忘一下吧。 最终的成品如下图所示,为了展示方便,所以Type-B端子那边没有用热缩管包裹。真正制作的时候是需要用热缩管对4条线的焊脚部分整体包裹、固定一下的: UP4000单板电脑的CN15接口线序定义如下: USB各个段子的线序定义: 最后再将焊接的示意图备忘一下。这张图右下角的手绘部分,其实更好的应该用手绘板,但是我实在犯懒、懒得起身,所以就直接用鼠标哆哆嗦嗦的画一下,估计自己今后看到的时候还能知道他们的对应关系(实际上恐怕很难,以我的经验而言,这种信手随便做的备忘,过不了多久自己再看的时候,就会忘记都是什么意思了。也许今后再做这个焊接工作的时候,我还是会再次重新回忆那边是Pin1、然后还要逐一核对这4条线是否正确)。
WordPress发布文章失败问题与解决
昨天完成这个博客的升级之后,想着不如顺便搞一搞当前这台服务器的SSL支持、利用CloudFlare提供的免费服务为当前网站开通SSL证书、并启用https协议访问的功能。 CloudFlare提供的免费证书非常容易申请,只要将域名DNS给到CloudFlare托管、便可以直接开启SSL功能。而且配置起来也很灵活、方便。用了不到20分钟,便令当前网站支持了https协议。 但是试用了一阵发现,WordPress出现了一些问题:前台文章访问、阅读等一切功能都正常,但进入后台之后,发布文章或修改文章时,会提示:Updating failed. You are probably offline。 这是因为后台发布文章时,wordpress会在服务器上直接本地调用自身的接口,而它尝试本地调用的使用也是采用https协议。但我并没有在服务器上部署证书、当初偷懒,只在CloudFlare上做了边缘证书。也就是说通过dns解析域名时,会经过cloudFlare进行中转,但在服务器上直接访问时却发现服务器实际上并未真实的支持SSL协议。 解决起来也简单:对wordpress进行一些修改,让它在进行文章发布、更新时,仍然使用http进行访问。不过这样的修改工作量其实远比做一套完整、完备的端到端证书要更加繁琐。而且同样的工作量下,这样一种“修修补补”的方式反而会给自己日后升级blog埋下隐患。 所以,既然服务器的权限完全在自己手里,又能够对apache进行各种配置、调整,就没有必要只做一个边缘证书,而是中规中矩的在CloudFlare中申请一套免费证书、并且下载到服务器上,开通apache的ssl mod,并将证书文件指定好,如此一番操作下来,彻底完成当前web server的端到端加密访问支持。 重启apache服务,一切正常,无论wordpress的前台还是后台功能,就都正常了。 后记:利用CloudFlare提供的免费证书完成服务器的ssl支持,还是非常简单、容易的。我起初对这个流程并不了解,在网上搜索他人教程,发现写的也是五花八门、迂回曲折。但自己真正的一条路走下来,发现整个过程并不复杂,现在想着自己手里还有另外一个小网站也是多年没有维护、还停留在http访问方式上。 待过些日子,对那个网站也做一下SSL的支持,到时将完整的配置过程,逐步截图留存,并写一个step by step的图文,当给同样遇此问题的朋友们参考吧。
Blog升级到了最新版本
这个Blog很久没有更新过了,使用的WordPress也一直停留在5.1.12未曾更新,今天下定决心将它升级一下。 升级的想法我已经动过很多次,但每每想起来,就觉得麻烦。原因是这台服务器上的PHP还是5.6版本,因为WordPress的新版已经需要至少PHP7.1才能安装,所以不得不从基础环境入手,我一直觉得那可能会是非常繁重的工作。 不升级吧心里总是惦记着,升级呢又担心麻烦。今天我终于鼓起勇气,决定大刀阔斧地进行一下升级工作。结果却发现整个过程远比想象的简单,很快就都搞定了。 首先服务器的系统,重新安装了一遍。没有使用自己常用的Ubuntu,而是改用AWS推荐的Amazon Linux。我想既然是跑在AWS上的服务,用他自家的系统应该更好一些吧?而且接下来公司的一些项目可能要用到AWS的服务,提前了解一下Amazon Linux也许是必要的。 其余的LAMP模块都还是中规中矩,直接用包管理器一键安装,很快就都搞定了。 最后将老Blog部署上去,并将WordPress的最新版下载、解压、覆盖、升级,便完成了所有的工作。 以上全部,连40分钟都没到就全都完成了。早知道这么容易,早就该升级才是。 上面的WordPress升级完成之后,我想不如趁热打铁,将另外一个拖欠了很久的工作一并做了吧:给当前的博客增加支持HTTPS访问。 以前要想个人拥有一套SSL证书,是比较难的,主要是因为这个证书资源太贵了,最便宜的一年恐怕也要几百元。如果脱离证书颁发机构自己直接发行一张证书、又完全没有意义——浏览器会提示这个证书并非公信机构发行,这个警告提示一旦显示出来,会让人觉得网站是不是被黑了、效果反而更差。 如今SSL证书的获取相对就比较容易了,有一些机构为了扶持个人网站的发展,提供了免费的证书。例如cloudflare,我就用这个公司对当前博客的域名进行了托管,并且使用他提供的免费证书完成了当前网站对https访问的支持。 不过因为WordPress似乎对https访问的支持存在着一些小的问题,所以这块的工作进展并不是十分顺利,虽然现在磕磕绊绊的算是可以正常访问,但感觉其中还是或多或少存在着一些问题,只待再有时间、再完善吧。
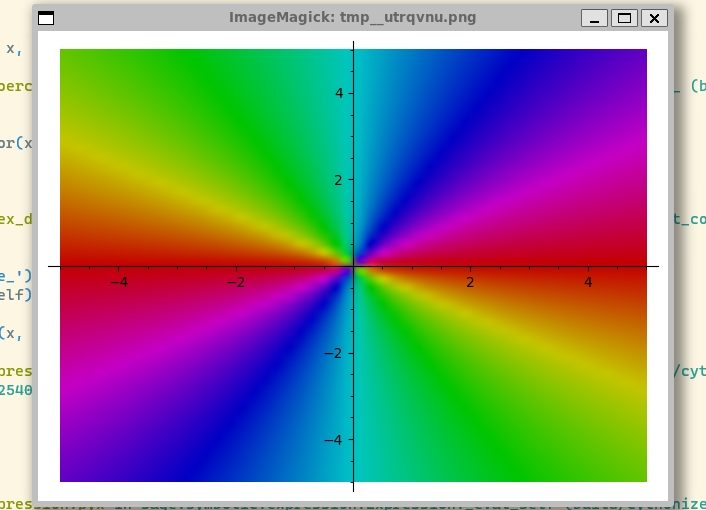
函数的图像
试使用SageMath进行函数图像的绘制。例如:对于复变函数 上面函数,可以使用SageMath绘制出在复平面上的图像: 其中的complex_plot()和plot()相似,只是声明为在复平面上进行绘图。后面的第一个(-5,5)指实坐标范围从-5到+5,第二个(-5,5)指的是虚数坐标、也就是复平面上的纵坐标、从-5i到+5i。 绘制出来的图像比较“抽象”,大概能看出来是通过彩色的衔接来表达是否连续,但这五颜六色的色彩对我而言还是比较陌生、一时难以理解的。 生成的图像是: 上面的图象太模糊了,改变参数,调整为plot_points=500,可以得到更清晰、精致的图像:
数学家的故事——布尔
此文写于2017年12月29日。 真假话游戏您接触过吗?话说: 有甲、乙、丙三位精灵,其中一位永远说真话、一位永远说假话、还有一位随机地给出真话或假话。您可以向他们发问三条是非题,每条问题只能问一位精灵,最终推理出谁说真话、假话,谁是随机答话。而精灵们只会回复“嘀”或“嗒”,但你并不知道它们的意思,只知道其中一个字代表“对”,另外一个字代表“错”。该如何发问、如何推理? 三个精灵真假话问题 上面这道有趣的逻辑推理,有时间不妨试算一下,不过我们今天并不是做推理游戏,而是要来说一说这些推理背后的故事。 上面的推理大家都知道叫做“逻辑推理”,但是该如何推理并不是所有人都了解的,只有学过逻辑学和布尔代数的人才能够进行解答。这其中的布尔代数,就是我们今天故事的主角。我们来八一八它的创立过程。 布尔代数,听名字您就能够猜到,它是根据一位名叫“布尔”的人来命名的运算体系,这个人全名“乔治·布尔”,是一名出生于英格兰的数学家。 乔治·布尔和很多有名的数学家不同,他不但没有接受过系统的数学训练、身为鞋匠之子的他甚至只有小学毕业而已。但鞋匠父亲恰巧也十分迷恋数学、并且布尔自己很努力,在父亲的帮助和自己的努力下,布尔通过自学在数学领域进行了自我深造。 在他17岁左右的时候,因为家庭原因,他必须要考虑工作,因而导致他连继续自学的时间都没有了。起初布尔考虑承袭父业做一名鞋匠、也考虑过做当地的牧师、还在当地的学校中做过兼职授课,不过最终他选择了自己创办一所学校,于是在1835年的时候,布尔创立了一所小学校,从此便以教书为生。 布尔创立自己的学校之前,因为有着很深的数学情节,所以业余时间继续以钻研数学为主。他在给学生们授课的同时,自己也在深入的研究当时主流的数学热点——微分、变分等知识。偶尔也会发表一些自己的论文,也正因如此,他并没有与主流数学界脱节,反而由此认识了更多数学界的专业学术人员。 随着布尔对逻辑学方面的深入研究,他在符号逻辑这一数学分支上的贡献也越来越多,终于在1849年被任命为爱尔兰皇后学院的数学教授。在经历了几年的教授生涯之后,布尔最终著作出版了《The Laws of Thought》。 这本书中最重要的贡献之一,正是布尔仿照代数运算创立出的一套逻辑运算体系,并以自己的名字命名——布尔代数。布尔代数看上去十分的简单,参与运算的数值只有两个:1或者0;所能进行的运算也只有三种:与、或、非。这套全部构成只有5个符号的数学,看上去如此的“迷你”,甚至有人怀疑它能否被称为一套体系。 事实上,布尔代数在提出之后也的确没有被主流数学界所重视,人们当时更认可的还是布尔在诸如微分方面的贡献。直到布尔逝世73年之后,一位名叫“克劳德·埃尔伍德·香农”的小伙子(详见《数学家的故事——香农》)无意中发现电子回路与继电器开关状态可以借助布尔代数来构建模型、还可以利用布尔代数进行电话交换机最优解的求解,从此才令布尔代数进入了主流数学界的视野。 布尔的成功不仅是他从鞋匠之子自学成为数学教授的励志过程,更多的,在我看来是他家庭和养育子女的成功。布尔在进入到爱尔兰皇后学院不久,碰到了一名美丽的、比自己小17岁的妙龄少女Mary Everest(可不要小瞧了这个女人,她后来也是一位非常有名的女数学家),并且很快确立了恋爱关系直至结婚。婚后他们生育了五个女儿,令人感到敬佩的是他们的5个女儿也巾帼不让须眉,各个都是有名有望的人。 如果您不爱好数学、而是偏爱文学,那么您是否读过经典文学《The Gadfly》呢?没有读过吗?这本书的中文译名叫《牛虻》,这本书的原作者可就是布尔老先生的小女儿Ethel Lilian! 先不聊布尔的女儿、外孙这一大家子世界名人,暂且说回布尔的妻子,提到美丽的Mary,就不得不说到“布尔之死”了,Mary Everest虽然在数学上拥有着和布尔一样的天赋、而且在家庭教育方面也十分的杰出。然而她却有着和大多数数学家一样的木讷,学术的高智商也导致了她在某些方面无知到令人无奈…… 1864年11月底的一天,已经50岁的布尔老先生从家中步行去学校授课,那一天下着大雨,布尔傻乎乎的没有打伞就出门了(数学家都木的如此令人抓狂么?)。一路走到学校之后身上已经淋透,他就这样穿着湿透的衣服给学生们上课。 结果可想而知,回到家中的布尔生病、发起了高烧。更令人惋惜的是他那美丽、木讷的妻子坚持相信“以毒攻毒”的治病偏方,她让自己的丈夫躺在床上,然后就一桶桶的凉水直接倒灌在布尔身上,经过这么一折腾,布尔的病情加重、并最终于1864年12月8日,因肺炎引发积液而病故。 上文已经提到,在布尔去世后,布尔代数并没有继续被主流数学界所重视,直到73年之后香农的研究中依靠布尔代数来创建电路模型、再后来就是大家所熟知的,图灵提出了图灵机的理论概念、冯·诺依曼进而制造出了电子计算机、一路发展到乔布斯发布了iPhone…… 如此看来,我们今天能够使用电脑、上网、访问今日头条、Bilibili、甚至您在阅读这篇文章,想一想其中都有着乔治·布尔做出的贡献。
数学家的故事——卡尔丹
文章写于2017年12月28日。 如果设有x²+2x+1=0等式成立,让你来求解这个方程式中的x,想必多数人都能不费力的通过配方法使原方程转化为(x+1)²=0,进而推出x应该等于“-1”。 但对于x³+3x²=5这个方程,还有谁能尝试着解出x来么?经过一些努力和尝试,恐怕不少人都会放弃了吧? 上面的两个方程,都只有一个未知数,所以都被称作“一元方程”。第一个方程中的未知数最高次幂是2,所以将它叫做“一元2次方程”;第二个方程相应的被称为“一元3次方程”。 二次方程对我们而言并不陌生,中学的时候就已经学习过二次方程的配方求解法,也就是将方程左边转化为一个完全平方、右边是一个常量,然后再利用开平方便可轻松求解。 但我们并没有学过三次方程的求解方法。事实上,三次方程的解法要比二次方程复杂许多、复杂到直至1545年前后,才被数学家们找到求解的方法。而在那之前,根本就没有人能解出一般形式的三次方程。 1545年,一本专论代数学的著作《大法》的出版,才使得人们知晓了三次方程的解法。 由此看来,我们真应该感谢《大法》一书的作者——哲罗姆·卡尔丹,似乎是他教会了我们三次方程的求解过程。 科学界的确给予了卡尔丹很大的肯定,以“卡尔丹公式”来命名了这个三次方程的求根过程。 然而,对卡尔丹的肯定恰恰是对另一位数学家的不公。没错,卡尔丹并不是“卡尔丹公式”的发明人,他不仅不是这一解法的创造者、甚至可能是个剽窃者,这一切都要从1494年说起…… 1494年,意大利方济各会的修道士帕西奥里(这个人来头可不小呢,他被视为现代会计之父,详见《数学家的故事——帕西奥里》一文)出版了一本《算术,几何,比,比例的摘要》,其中广泛的讨论了各种二次方程,然而却对三次方程只字未提。 原因是帕西奥里认为三次方程是不可求解的。他的这一观点显然不被当时的数学界所接受,当时有不少的数学家都在疯了心、玩了命、努力的尝试找寻三次方程的解法。这是数学家们的竞赛、是一场智者们的游戏。 大约在1505年,博洛尼亚的数学学会会长弗罗宣称找到了三次方程的解法。他虽然宣布找到了解法,却并未公开任何的求解过程。这种一厢情愿的宣布可不能记入史册,谁能担保他不是在吹牛?然而这却鼓舞了很多的数学家,大家更坚信三次方程是存在着求解方法的。 既然弗罗没有公开细节,那么大家就都还有机会继续这场竞赛。 受鼓舞的人中,有一名年轻的数学家,大家不喜欢叫他的名字,而喜欢叫他的外号“结巴先生”。 “结巴先生”认为数学会长不可能信口胡说,既然敢宣布,那么三次方程的解法就一定存在。于是“结巴先生”更加专心勤奋的研究。没用多久,“结巴先生”便也对外宣布自己找到了三次方程的解法。 有趣的是,“结巴先生”和弗罗一样没有将解法公开。此时你就知道本文开头那道三次方程想解出来有多难了吧?它曾经可是难倒过数不尽的数学家们呢。 “结巴先生”和弗罗都不公开细节,这下子其他的数学家们都不能开心地玩耍了。你们俩人都说拥有三次方程的解法、可又偏偏都不公开,这说出来不是骗鬼呢吗? 虽说不公开核心解法的做法可以理解:毕竟持有核心算法的人能够在相关领域比别人研究的更深、走得更远。但谁又能证明他们真的有能力解开三次方程、三次方程真的是一个可求解问题呢? 为了证明三次方程确实可求解,有人组织了一场“结巴先生”和弗罗的二人比赛,提出一些三次方程,看两人谁能给出正确的答案,又或者都能给出或都做不出来。 比赛在二人之间展开,结果稍稍出人意料:“结巴先生”轻松的胜出了这场比拼。这一结果令弗罗多少有些颜面扫地。 更重要的是,“结巴先生”用实际行动证明了确实有三次方程的解法。只不过大家还是不知道具体解法过程,因为“结巴先生”依然不愿意公开其推演过程。 若是“结巴先生”此时公开推演过程,不仅可以名利双收,同时也不会再有接下来的故事。可我们亲爱的“结巴先生”就是惜字如金,一个字也不愿多“说”。 这时本文的主角卡尔丹出场了。卡尔丹也是一位有名的数学家,他更为人们津津乐道的是他喜欢赌博,是一名善用“概率”的赌徒。 当时的卡尔丹对三次方程也十分着迷,进行了很长时间的研究。当卡尔丹听说了“结巴胜出”的消息时,便迫不及待的登门拜访,希望“结巴先生”能分享一些经验给自己。 结果可想而知,“惜字如金的结巴先生”直接拒绝了卡尔丹的请求,一丝一毫的信息都没有透露。 卡尔丹在遭到拒绝后并没有放弃,这位拥有着任何赌徒都有的执著性格的数学家,真的是执著到了偏执的境地,他几次三番的拜访、一次次的登门、大有不达目的决不罢休之势。…
苹果1984年时的宣传海报
这是1984年在苹果产品发布会上出现的海报,当时乔布斯就在会上立下一个志向:要令这台电脑成为继电话之后的、第二款桌面设备,为人们所熟知。今天看来,苹果当时对未来市场的眼光,无疑是十分正确的。 1984年时,不要说是互联网、就连电脑也十分的罕见,当时撩撩几家电脑生产厂商都是在销售着价格昂贵的商业计算机,个人微机的概念在当时恐怕很少有人敢想——计算机可不是一般老百姓想拥有就能够拥有的。 在当时,电话已经普及、并且真真实实的成为了人类历史上第一款“桌面电子设备”。与电话不同,当时的电脑,还是一个“高大上”的物件,很少有人能够接触到。 那时的美国大约有2.35亿人,其中能够知道并接触到电脑的人还凤毛麟角,除了商业用户和军用外,一般老百姓中只有对电子技术十分着迷的人乐忠于“捣鼓这些闪烁着灯光的电线”。 而苹果公司、乔布斯,当时便锁定了2.35亿人中的10%——也就是2500万人,他认为,这2500万的“办公室白领和大学校园中的学生”,将会是未来在电脑普及之后的主要使用人群,也就是说电脑将成为继电话之后的第二个“桌面电子设备”。并且个人微机的时代已经到来,因为苹果自己推出的电脑,就是专为这2500万人打造的。 所以基于以上的市场定位和对未来的预期,苹果推出了这款“小巧便携、可以为个人用户所用的”Macintosh(麦金塔)、也就是今天我们所熟知的“Mac电脑”。 这张海报上的宣传语“Of the 235 million people in America, only a fraction can use a computer”,是当时发布会上的一句演讲词,这句话的完整表述是: Because of the 235 million people in…

