
又新买了一个USB网卡
1. 之前本来有一个USB网卡,但是被朋友“借走了”,只好再新买一个。之前被朋友借走的是“绿联”,最近因为“囊中羞涩”,所以只能买一个性价比更高的品牌——比亚兹。 我不太清楚这些不同的品牌、但是功能相近的小周边,本质上有没有品质和成本的差异,但是单从外观和使用体验上,暂时并没有感受到什么太大的差异。 可偏偏就是这样一个“没有差异”的感觉,却让我的心情十分不好。原因在于我又有些“替古人担忧”了。我总是觉得这种看似谁都可以做的小周边产品,应该有个更专注、更专业的品牌,那样才能令患有“购买焦虑症”和“选择恐惧症”的人,在购买的时候,不会有太多的左右为难——有钱的时候就买公认最好、最专业的品牌,没钱的时候买个凑合能用的临时将就一下。 没有,这种小周边、小电器,现阶段应该是没有谁家能说自己就是最专业的,大家都是你做我也做,他有谁都有,并不能通过参数、配置、指标分辨出好歹。所以购买的时候总会很纠结。更多的时候,这种商品的购买往往是通过“先入为主”在自己印象中给出它的归属。 例如电脑周边的小产品,我莫明其妙的就会觉得“绿联”非常好、非常专业。为什么会有这种感觉呢?说不好,似乎是“绿联”这个品牌的名字起的不叫正规、大气吧。
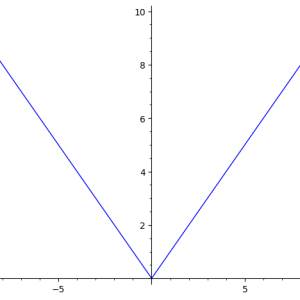
记一个自己学习初等数学“切线”时的困惑
一、我的困惑和不解 函数的图像如下,显然的,在原点处是没有这个函数的切线的。但这里“显然”似乎又不是那么“显然”,切线究竟是什么呢?对于在平面上的曲线的切线,历史上有过多种定义方式,现今对切线的定义与莱布尼茨给出的定义表述是一致的,都是利用极限的思想对切线进行定义。 对于曲线S上的某一点A,在A点外做另一个同样落在曲线S上的点B,这样AB可以构成一条直线L,这条直线L可以称为曲线S的割线。 当B点沿曲线移动、并逐渐向A点接近,也就是B沿曲线S像A点逼近,当时,得到的割线便是经过A点的曲线的切线。 上面的定义本来能够解答下面这个图象的疑问:为什么在图像的原点处,没有切线呢?答:因为如果设原点处为A,可以从图像上看出来,B点在左边和B点在右边两种情况下,当时,得到的“极限L线”不一致,所以原点、也就是A点处的切线是不存在的。 但是上面这个答案、或者说解释,以我现在的数学水平,是无法“透彻理解”的。原因在于: 1、我为什么不能说这一点上有2条切线?为什么偏偏要说这一点上的切线不存在?难道图像上任何一点只能最多只有一条切线吗? 2、并不是,而直线既然是通过A和B两点定义的,那么在时就不是严格的,此时通过极限得到的与时得到的就一定是一样的吗?这里额外的又回到了上面的问题:没有2个点,怎么定义出的直线呢? 不想了,想多了脑袋痛。我觉得想通过“极限”定义出切线,也许还有其他基础知识需要学习。换句话说,我隐约感觉:或者是我的学习脉络不正确;或者是这个定义的脉络不正确。也许应该先有导数的定义,有了导数的定义就有了斜率的概念、有了斜率和点A,就可以通过直线的另一个定义方式——点斜式——定义出直线。 所以如果按“将定义脉络翻过来”的想法来解释,也许就是:图像上某一点要先可导,当它可导时就是有斜率的,从而通过“点斜式直线定义”,这一点就是有一条“点斜式可唯一定义出的直线”的,从而这样一条唯一存在的直线就是该点的“切线”。 二、额外的问题: 在搜索上面的问题及尝试通过互联网找到答案时,看到网上有这么3句话: 1、在数学中,切线是与曲线在某一点相切的直线。更严格地说,曲线上某一点的切线是该点处的最佳线性逼近。切线的定义依赖于“可微性”的概念。如果曲线在某一点处是可微的,那么该点处的切线是唯一的; 2、如果曲线在某一点处不可微,则该点处的切线可能不存在,或者不唯一; 3、如果切线的斜率为无穷大,则切线是垂直的; 上面这三句话令我更加“头晕目眩”了。原本的问题没有得到解答,却又多出来更多的“读不懂且理解不了、想不出具体情形”的表述。我现在对数学学习的感觉就是:不要想太多,能把课后习题做出来,就知足了。
柯西-黎曼方程(C-R条件)学习备忘
一、历史 1、柯西-黎曼方程,也被称为C-R条件,全称是Cauchy-Riemann equations; 2、这是一个由2个偏微分方程组构成的系统,通过这个系统可以验证给定的复变函数是否可微。因为C-R条件用于验证指定方程是否可微,所以是一种“条件验证功能”,因而叫做“C-R条件”; 3、C-R方程最早可能是1752年时,由欧拉(Leonhard Euler)首次发现的,虽然他发现并记录了这个方程组,但并没有将这个“条件方程组”与“复变函数的可微性”联系起来; 4、到了1821年,柯西(Augustin-Louis Cauchy)证明了复变函数可微的必要条件是满足C-R方程; 5、再到1851年,黎曼(Bernhard Riemann)证明了满足C-R方程是复变函数可微的充分条件; 6、经过了上述3个阶段之后,C-R方程正式成为了复变函数可微的充要条件的验证依据。
三极管基极、集电极、发射极三个名称的含义由来
本文仅为个人观点 一、问题 三极管的三个电极各自有自己的名字,分别是:基极(Base)、集电极(Collector)、发射极(Emitter)。对于PNP型、NPN型三极管,他们的图示分别如下: 对于三个电极的命名,我一直比较混乱。虽然能够记住他们,但是脑海中却总是有种“毛毛躁躁”的困惑,说不清、也想不明白,为什么这三个电极要如此命名呢? 二、历史 1、1947年 PNP型三极管和NPN型三极管并不是在同一时间被发明出来的,而是在1947年12月时,NPN型三极管先被发明了出来,它是由William Shockley、Walter Brattain和John Bardeen等人,在AT&T贝尔实验室中发明、制造出NPN型三极管。 2、1948年 之后在1948年时,贝尔实验室的John R. Pierce和Lester Hogan两人在《The Bipolar Transistor – A New Type of Semiconductor Amplifier》论文中,首次使用基极(Base)、集电极(Collector)、发射极(Emitter)这三个名称。 注:这篇文章最初发表在1948年的《Proceedings of the…

解析函数例题1则
一、例题的出现 在《复变函数》最开始的部分,有一道例题,有如下两种表述方式: 例:证明:函数 在z=0点可导,且导数等于0。 或者另外一种表述方式: 例:讨论函数的可导性。 上面两种表述方式其实是一样的,针对的都是相同的函数,研究的课题也是一样的:求出它在点的导数。有趣的是,这两个表述方式都巧妙地避开了“不严谨”。 如果让我出这道题,也许会被写成:计算出的导函数,并求出的值。 按照我的设问方式,实际上也是可以正常进行这道题的求解的,但是“问法”相当于已经默认了这个复变函数是“处处可导”的了。上面的例题使用的设问方式就很“狡猾”,它们知道这个函数并非处处可导、只在时才可导,所以从最初的设问环节开始,就避开了“不严谨”的说法。 所以这道题按照例题的问法,至少应该从以下2个方面完成: 1、深刻的理解导数和导函数是什么,小心地求证原函数是否在指定的点处可导; 2、如果原函数并非处处可导,而只在部分区域上可求导。则要看题目要求的求导点是否在可导区间上(例如本例题要求在点得出导数值),在可求导区域内则进行求导、不在可求导区域内则不存在对应的导数。 二、函数可导、导函数的意义 个人理解:函数可导、有导函数,大意似乎是:这个函数连续、并且拥有连续的渐变光滑性,其中连续的渐变光滑性的意思就是他在图像上的每一个点上都有切线存在。 上面的说法如果正确的话,在实函数上是可以比较方便的通过图像理解的。但是对于复变函数而言,图像上理解起来有一些吃力。我还不知道如何通过图像去理解这个事情(图1、图2)。 例如下图1,就是相关复变函数的图像,从这个图像上能看出函数的确是连续的、并且是渐变的,如果它的导函数也是连续的、渐变的(所有的色彩过度都是渐变衔接),那么这个函数就是有导函数的。但是从图2来看,这个函数的导函数并不是在每一个区域都是渐变的,它只在所有的横坐标上有着渐变色彩,而在任何一个纵坐标的垂直线上,都是“固定单色”,不在拥有色彩的渐变性。因而大概猜测,这个函数的导函数是不存在的。 图像1:函数的图像 图像2:函数的图像 三、除z=0点外,其他地方不可导 “深色教材”的P17页就是上面的例题,但是我还是没有完全理解。整体意思就是它最终得出的结论就是,在除了z=0的点以外的地方,导函数的值都不存在极限,因而也就不可导。具体的求证过程如下: 已知函数 ,此时,由导数定义可知 情况1:当时,上式很容易看出来是趋于0的,所以极限存在、且是0; 情况2:当时,上式的极限将等于。此时第二项中的“分数”是多少呢?这里就要再展开详细的推敲一下,也就是产生了一个新的子问题: 子问题:已知,求 五、当时,求 上面已经将问题转成了新的问题,现在对这个新的问题进行推导。书上这个过程是非常简略的,但是我数学基础差、脑子也不好使,所以展开一点点的推导。…

专注于斐波那契数列研究的期刊
Fibonacci Quarterly是由Fibonacci Association主办的一本期刊,专注于对斐波那契数列(Fibonacci)及相关的数学领域进行研究。它的网站是:https://www.fq.math.ca/ 在它的网站上提供了从创刊的第1卷起,至第47卷(1963年-2009年)的全部电子版期刊,从48卷之后发布的期刊虽然不再提供全文、但也仍然会提供摘要版本。 我对斐波那契数列相关的数学知识并不感兴趣、工作中也几乎没有与之相关的工作,但是因为业余生活中比较喜欢看数学方面的科普文章,所以对这个数列知道一些有趣的故事。 斐波那契数列是由1202年斐波那契收集阿拉伯和希腊的数学研究资料、编撰整理出来的《算盘书》中一个有趣的“兔子问题”引申、发展出来的。在《算盘书》中,斐波那契提出了一个“兔子问题”:假定大兔子每月生一对小兔子,而小兔子经过两个月就可以长成大兔子,那么自拥有一对大兔子开始,一年后可以繁殖多少对兔子? 上面这个兔子问题,如果绘制成表格: 从这个表格上可以看出来,无论是大兔子的数量、还是大兔子当月诞下的小兔子数量、还有每个月新长大的小兔子数量(从3月开始),都是相同的数列:1,1,2,3,5,8,13,21,34,…… 这个数列就是“斐波那契数列”,它从第三项开始,每一项都是前两项的和。如果用计算式表达,可以表示成:。 这个数列以及它的第n项的表达式,看上去都似乎平平无奇,然而如果要想将它的第n项表达式写成通项公式便不是那么简单的事情了。事实上,它的通项公式是自1202年斐波那契数列提出之后,经过了600多年、直到1843年才由法国数学家雅克·比奈(Jacques Philippe Marie Binet)归纳出来,因而这个通项公式被命名为Binet公式:。 Binet通项式有趣的地方有两个: 1、首先是一目了然的:它其中含有无理数,这实在是令人感到不可思议。一个简单的、完全由整数构成的数列,竟然需要使用无理数构造它的通项式。实际上也的确如此,如果不是引入了无理数,那么也不至于经历了600多年才被比奈归纳出来; 2、另一个有趣的事情可以看出来,当斐波那契数列趋于无限大之后,它的前后两项的比值趋于 。而这个比值恰恰是黄金分割比例0.618…… 斐波那契数列除了上面这些浅显的常识之外,还有很多重要的应用,无论是在计算机、密码学;还是在金融与经济学;又或者在物理和工程学上,都能见到它的身影。也正因为如此,回到本文开始提到的网站,才会有专门的这个专刊,定期刊发有关斐波那契数列的最新研究成果和消息。 update 2024.11.10 1、最近闲来无事阅读《数学史》,看到其中也有关于斐波那契的历史介绍。其中提到斐波那契生活的公元1200年左右恰是欧洲文明的“黑暗时期”,那时的欧洲非常荒芜、落后,并没有后来文艺复兴时期的辉煌璀璨。可以说是人类历史上的蒙昧时期; 2、前几天自己因为记不住牛顿二项式展开,所以手动推敲了一遍。其中也用到了一个数列,不过并非斐波那契数列、而是杨辉三角形。我因为以前并不知道斐波那契数列,所以误以为杨辉三角形就是斐波那契数列,今天才知道两个数量完全风马牛不相及。
RC振荡电路初学笔记(5)
我放弃了基于PNP进行RC振荡电路的学习,原因是以PNP做核心放大的文章实在是太少了。网上全都是以NPN作为放大器进行介绍的,所以我也先按照NPN来学习。等到对振荡电路理解透彻之后,再推敲改成PNP后有什么区别吧。 1、之前电路图的错误: 首先是之前自己胡乱画出来的基于NPN的电路,严格来说都是错误的:RC反馈网络并不是如我之前画的那样需要3个去地电阻(这篇文章中的插图就是错误的,注1),而是只需要2个去地电阻;额外的还需要一颗串联电阻。所以正确的电路图今天依照《这份材料》实现。 2、频率的计算: 这个地方比较郁闷,因为对于这个电路而言,频率无论使用下面哪个公式进行计算,都是与实际仿真有较大差别的: 使用CircuitJS仿真结果是9.524KHz,使用LTSpice仿真结果是9482Hz。可以看到CircuitJS和LTSpice的计算结果是一致的,但与我的笔算结果都是相差很大的。这是什么原因呢? 注1:其实也不能算是错误,因为网上也有其他材料中,反馈部分都是各自有各种各样的不同,所以估计也不是错误,只是自己还不理解其中每一个IC的作用,还要再花时间了解、学习。 注2:Jacob Millman和Arvin Grabel合著的《Microelectronics》一书中,应该是有比较详细的RC相移振荡器的介绍的,图书在这里 Microelectronics: Jacob Millman, Arvin Grabel 。可惜我手中其他基本别人著的《微电子电路》的图书中,都没有这个电路的详细讲解,有一些郁闷。 update 2024-11-11 时隔5个月,上面的问题终于有了一些小的进展。首先是完成了《RC振荡电路初学笔记(6)》的学习和学习笔记整理,其次是今天晚上终于搞清楚了频率的计算方法,不过还没有时间将今天的笔记整理出来。
RC振荡电路初学笔记(4)
想基于Jack Kilby的电路文档学习RC相移振荡器是有一定的难度的,主要是因为他当初设计的电路是基于PNP核心,而今天我所能找到的RC相移振荡器的文章,都是基于NPN为核心讨论。 所以我想应该先把基于NPN的RC相移振荡器了解一下,才有可能推敲出Jack Kilby的电路的工作原理。 一、题外话:为什么要用PNP而不用NPN? 这里有一个额外的话题:为什么Jack Kilby要基于PNP做这个RC相移振荡器的集成电路呢?首先排除最不可能的原因:PNP在1958年的时候,没有NPN成熟。这个猜测是错误的,实际上晶体管从诞生之处,就是NPN先成熟起来,无论是制造工艺的成熟、尺寸的小巧、成本的低廉,都是NPN更胜一筹。所以没有道理不使用NPN。 那么Jack Kilby当年为什么不用NPN、而使用PNP呢?查资料,没有答案。各种资料随便整合到一起的猜测如下: 1、Jack Kilby进入TI实验室之后,并不是研究基于硅基片的晶体管工艺,他做的研究是基于锗基片进行生产; 2、Jack Kilby的工作,也许是只得到了PNP的研发权限,没有NPN的研发权限(这一点是猜测); 3、Jack Kilby的发明研发工作,也许需要避免向其他技术科室索取硅基片或NPN技术(也是猜测); 4、对于相同的电路模块,PNP电路也许在稳定性上不如NPN,但是从使用的IC数量上也许会少于NPN; 综上四点,也许就是Jack Kilby使用了PNP做核心元件的原因吧。 二、还是题外话:为什么NPN更优秀? 无论上面的第一点是怎样的情况,在今天我都遇到了一个新的困惑:为什么我能找到的RC振荡器的教程,都是基于NPN的、而没有一篇是基于PNP进行阐述的? 另外,从现在的结果上来看,似乎NPN更稳定,但究竟更稳定在哪里呢? 三、基于NPN的RC相移网络振荡器 这里有一些问题,先罗列出来: 1、反馈网络的两种形式: 反馈网络既可以是电阻串联、上面并联电容器;也可以是电容串联、上面并联电阻器。通过仿真,我也尝试出了两种不同形式的电路。如下图所示: 值得注意的是,两种形式在通过RC网络计算输出频率时,使用的公式是不一样的。 电容串联时(常见形式):…

陪家人,逛漫展
今天陪老婆、孩子一起去首钢园逛icos漫展,目测现场至少6000人,规模宏大、场面壮观。满场的俊俏,赏心悦目。 老婆喜欢国乙、大儿偏爱原神、小儿还没到挑剔的年龄,只要好看好玩的新奇都有着十足的兴趣。我满心期待能收获一些手办,结果现场主题是cosplay,商家寥寥,心愿落空。好在美女如云也算饱了眼福。 漫展是在原焦化厂改建的首钢会展中心举办,群明湖畔、五一剧场附近,那里的一切对我而言,并不陌生。 小学时,每年都会去五一剧场“红五月歌咏比赛”,我五音不全只能滥竽充数。对于小学生,当众表演本就十分紧张,只开口不发声更增加了惶恐,所以不用任何的粉饰,我的脸就已经通红到了耳垂。老师并不会考虑到这个因素,在入场前总会给我们涂上浓重的腮红和口红。现在回忆起来,还能感到脸颊阵阵发热。 父亲喜欢钓鱼,盛夏时总会带我去群明湖。父亲钓鱼时、我用铁丝圈套蜘蛛网,等蛛网套上几层后,便会在湖畔粘蜻蜓。运气好时能粘住个头巨大的“老干儿”,那会让我兴奋的手舞足蹈。可父亲总会十分严厉的告诫我要小心,骗我说湖水深不见底。我是相信的,因为任人看过那个人工净水湖,就会想当然地以为它是个“倒金字塔型”,一旦落水就会一路滑入湖中心、巨大的深渊。 焦化厂并不像五一剧场或群名湖,那是闲人免进的厂区。从围墙外远远的,便能看到六座巨大的料仓,如首钢厂区内其他巨大的仓、釜、塔、罐……这些远超常规尺寸的巨大设备,与周边的建筑形成鲜明对比,有种巨物压迫感、像是来自外星的科技、十分恐怖。 火车穿行于首钢各个厂区之间、铁路从外部直通整个厂区,将各类原材料、成品,送入、送出。我家村子就在首钢边上,村里的小孩儿每逢放假就会去铁路周边玩耍:抓蜻蜓、逮蚂蚱……更多的时候,则是三五成群,沿着铁道捡拾散落在草丛里的各类“宝贝”,不知是送入还是送出焦化厂的焦炭,便是我们共识的宝贝之一。 拿着蜻蜓跑回家,往往会被莫名的踹上几脚;但如果拎着一箩筐、哪怕其中只有3、5块的焦炭回去,无论是在草地里打过滚儿、还是和小伙伴彼此往对方脸上抹过泥,都会因为帮家里寻得了“宝藏”而免受皮肉之苦。 再去首钢园,儿时回忆不禁涌上心头。
电容电压计算过程中的小困惑已经解决
一、初期问题 在之前的文章中,我尝试自己推导出电容被充电时,电容上的电压变化过程。 起初因为在等式变换过程中搞错了一个“正负号”,结果无论如何也推导不出来。并且因为这个“正负号”的错误很难看出来,所以一直被卡住。 昨天晚上又仔细地推敲了一遍推导过程,搞清楚了自己把正负号弄错的原因: 等号左边我做了一次分母两项调换、等号右边就应该相应的增加一个“负号”,但是忘记了。等到想起来要在右边增加符号的时候,又想当然的认为应该在等号两边同时增加负号。 这就导致了从一开始左右因数就差了一个“-1”,后来自以为的找到了问题时左右同乘-1后,其实还是左右相差一个“-1”。 所以这就令我误以为:无论是否找到了错误、修正了错误,都无法正确的完成推导。其实本质原因是:我找到了错误,但是修正之后还是错误的。 二、关联问题 在等式存在错误的阶段,我尝试基于错误的等式先完成后面的推导过程。这里其实是存在隐患的:基于错误的等式继续往后做不定积分计算时,只能在常数项在等号右边时,才能令结果与正确结果错得不多、如果将常数项放在等号左边,会令计算结果错的非常离谱。 因为有了上面的结论,我就想当然地认为:纵使今后找到了问题、修正了问题之后,常数项也只能放在等号的右边。 于是我就在上面的“假象”下,认定了:常数项必须放在等号的右边。于是进一步的:我就开始怀疑起原因:为什么常数项只能放在等号的右边呢? 其实上面所有的现象和想法,都是被误导了的。 在真正的找到了那个该死的“负号”错误之后,今天我分别将常数项放在等号左边、放在等号右边,都是可以正常完成推导、计算、得出相同的结论的。 所以这就解释了:不定积分得出的常数项,无所谓放在哪里,都是可以的。