两道题目如下:
1、计算:\(\lim_{x \to \infty} \frac{sin(x)}{x}\)
2、求证:\(\lim_{x \to 0} \frac{sin(x)}{x} = 1\)
一、计算:\(\lim_{x \to \infty} \frac{sin(x)}{x}\)
解法1:极限定理法
当x趋于无穷时:分子是个正弦反复跳跃、极限不存在;分母x趋于无穷、极限也不存在。因而分子和分母都没有明确的极限值的情况下,无法用商的极限运算法则进行计算。
考虑使用乘积的极限运算法则进行计算:\(\lim_{x \to \infty} \frac{sin(x)}{x} = \lim_{x \to \infty} sin(x) \times \lim_{x \to \infty} \frac{1}{x}\)。
分解出来的两个因式的结果分别是有界函数和无穷小,他们的乘积等于0。
解法2:三明治法
因为\(-1 \le sin(x) \le 1\),所以\(-\frac{1}{x} \le \frac{sin(x)}{x} \le \frac{1}{x}\)
左边有:\(\lim_{x \to \infty} -\frac{1}{x} = 0\)
右边有:\(\lim_{x \to \infty} \frac{1}{x} = 0\)
不等式两端在x趋于无穷时,同时趋于0,所以中间的极限\(\lim_{x \to \infty}\frac{sin(x)}{x} = 0\)
二、证明:\(\lim_{x \to 0} \frac{sin(x)}{x} = 1\)
这个证明比较难、甚至是非常难。虽然在《高等数学》和《普林斯顿微积分读本》的开始、最基础的章节中就有这个重要极限的介绍、以及证明。但实际上这两本书都故意忽略了一个基础极限:\(\lim_{x \to 0} cos(x) = 1\)。
在《高等数学》§1.7中,这里几乎是“一笔带过”假装“显而易见”糊弄过去了;在《普林斯顿》§7.1.5中则是给出了上面\(\lim_{x \to 0} cos(x) = 1\)的结论而也语焉不详的糊弄过去的。
两本书用的证明方法相同、也都忽略了上面提到的基础,我也先忽略、假装\(\lim_{x \to 0} cos(x) = 1\)是个事实,完成证明:基本思想依然是利用三明治定理,设法找到\(f(x) = \frac{sin(x)}{x}\)两边的函数,通过两边的极限,夹近出\(\lim_{x \to 0}f(x)\)的结果。
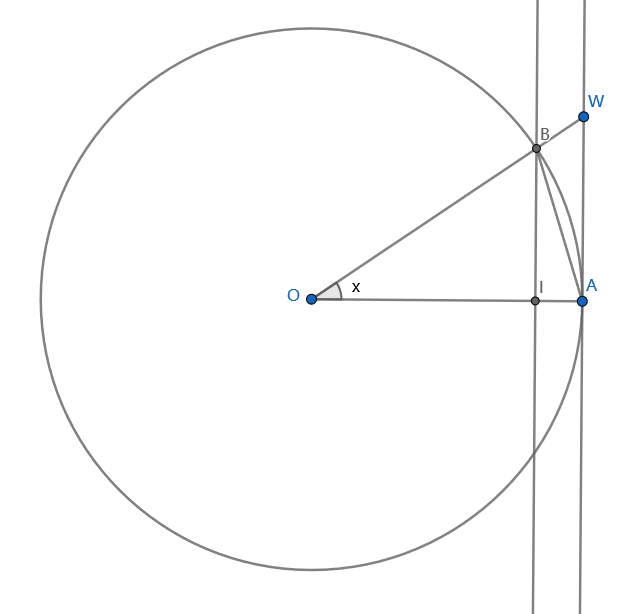
构建如上图形,其中圆为单位圆、半径\(r=1\),可以看出:\(S_{\Delta OAB} < S_{sector OAB} < S_{\Delta OAW}\),这个不等式的左中右分别为:
左侧:\(S_{\Delta OAB} = \frac{1}{2} |OA| |BI| = \frac{1}{2} |BI| = \frac{1}{2} sin(x) \)
中间:\(S_{sector OAB} = \frac{\pi r^2}{2 \pi} x = \frac{1}{2} x\)
右侧:\(S_{\Delta OAW} = \frac{1}{2} |OA| |AW| = \frac{1}{2} |AW| = \frac{1}{2} tan(x)\)
带入不等式,得到:\(\frac{1}{2} sin(x) < \frac{1}{2} x < \frac{1}{2} tan(x)\),
将这个不等式各个部分除以\(sin(x)\)并颠倒分子和分母、简单整理之后得到:\(cos(x) < \frac{sin(x)}{x} < 1\)
左侧:\(\lim_{x \to 0^+} cos(x) = 1\),注意这里是“假装显而易见先糊弄过去”;
右侧:\(\lim_{x \to 0^+} 1 = 1\),
通过三明治定理,即可夹近出中间的极限:\(\lim_{x \to 0^+} \frac{sin(x)}{x} = 1\)。
注意上面的三明治极限都是取的\(x \to 0^+\),这是因为原式\(\frac{sin(x)}{x}\)中的分母不能取0点,因而要分别求它的左极限和右极限,上面只是在计算右极限。相应的进行符号斟酌、调整,可以再求出左极限:\(\lim_{x \to 0^-} \frac{sin(x)}{x} = 1\)。
这样最终可以分别得出:\(\lim_{x \to 0^+} \frac{sin(x)}{x} = 1\)和\(\lim_{x \to 0^-} \frac{sin(x)}{x} = 1\)两个结论。左极限和右极限相等,最终确定它的极限存在,并且是:\(\lim_{x \to 0} \frac{sin(x)}{x} = 1\)。
三、遗留问题:关于\(\lim_{x \to 0} cos(x) = 1\)
之所以说这个问题“非常难”,是因为其中假设了一个“显而易见”的\(\lim_{x \to 0} cos(x) = 1\),其实它并不是显而易见的。这个极限需要用到泰勒近似,而泰勒近似是泰勒展开式的内容,泰勒展开式又是泰勒级数的内容。
而泰勒级数是“微积分”课程中,在完成极限、导数、微分、积分、级数这五部分循序渐进的知识之后,才谈到的知识。所以这有点儿像“贪吃蛇吃自己的尾巴”,所以只能先假设它是显而易见的了。
1、直观的、显而易见的结论:
如果从 \(f(x) = cos(x)\)的函数图像来看,这个函数在原点附近的确是连续的、无瑕点的、光滑的,因而当它趋近于0时,其极限就是\(cos(0)=1\)。
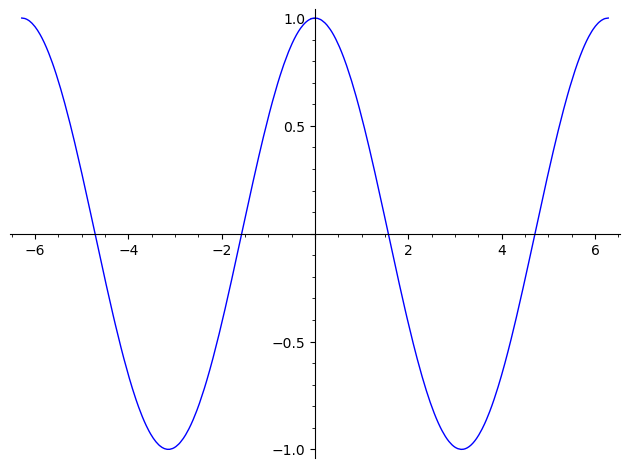
但是在有关函数极限的基础定理定义中,并没有这个“显而易见”的定义。所以如果严谨一些,还是应该通过推导、证明,才能得出关于它确凿为1的结论。
2、对\(\lim_{x \to 0} cos(x) = 1\)进行证明:
证明过程比较“难”,需要做一些初期的准备工作:
2.1、首先通过构建一个新的辅助函数用于巧妙地构建出可用于推导的机会。这就比较难,因为是“巧妙地构建出来”,需要的是灵感;
2.2、通过三角函数二倍角公式对上面“巧妙构建出来的”函数进行简化,将多项式转换成“单项式”。这里也比较难,原因在于“二倍角公式”一般情况下难以记住;
2.3、之后通过泰勒展开式对简化后的“单项式”进行展开,得到这个计算式的级数计算式。这里更难,原因是泰勒展开式基本是要等微积分课程的中后期才能学到;
2.4、对泰勒级数进行区段的划分,形成\(Result = P_N + R_{N+1}\)的形式,目的是通过这样的划分构建出不等式;
2.5、最后,通过上面得到的不等式,再次应用三明治定理,左侧极限与右侧极限相等进而得出中间的计算式的极限值。而最终中间极限就是原始极限,从而得出原始极限的最终结果。
只有通过上面的1-5步骤,才能确凿、肯定的得出\(\lim_{x \to 0} cos(x) = 1\)的结论。详细过程如下:
2-1、先构建一个新的函数 \(g(x) = 1-cos(x)\),并且期望证明\(\lim_{x \to 0} (1-cos(x)) = 0\),如果这个证明成功了,才可以确定\(\lim_{x \to 0} 1 = \lim_{x \to 0} cos(x) = 1\)。
2-2、利用三角函数二倍角公式对上述函数\(g(x)\)进行简化:\(g(x) = 1-cos(x) = 2 sin^2(\frac{x}{2})\)。这样就将欲证\(\lim_{x \to 0}(1-cos(x))=0\)问题,转换成了需证\(\lim_{x \to 0} 2 sin^2(\frac{x}{2}) = 0\)问题。
2-3、将\(g(x) = sin^2(\frac{x}{2})\)视为“三明治的中心”,找到可以夹逼它的下界函数\(left(x)\)和上界函数\(right(x)\)。因为g(x)的非负特性,所以下届函数可以直接使用常数;由通过泰勒计算,可得到他的上界函数。为思路连贯,先不考虑细节,直接得出不等式:\( left(x) < g(x) < right(x)\),即\( 0 < 2 sin^2(\frac{x}{2}) < \frac{x^2}{2}\)。
左侧计算式极限:\(\lim_{x \to 0} 0 = 0\),
右侧计算式极限:\(\lim_{x \to 0} \frac{x^2}{2} = 0\),
依据三明治定理,中间的函数极限便明确了:\(\lim_{x \to 0} g(x) = \lim_{x \to 0} 2 sin^2(\frac{x}{2}) = 0\)。
2-4、最后再将结论倒退着带回到原始问题中,原始问题也就得到了证明。
3、子问题:利用泰勒展开式得到不等式\(2 sin^2(\frac{x}{2}) < \frac{x^2}{2}\):
上面这个“子问题”,便是在同济版《高等数学》(第四版)中一笔带过的地方,它的推导思路是:首先利用泰勒展开,将含有三角函数的计算式\(2 sin^2(\frac{x}{2})\),展开成没有三角函数的多项式。而这个展开的多项式中恰巧包含着\(\frac{x^2}{2}\),这样便可以构建出上面的不等式了。
首先定义一个新的、简单的三角函数\(t(x) = sin(x)\),然后用泰勒多项式对它在\(x \to 0\)处进行展开,可以得到泰勒展开式是:\(t(x) = sin(x) = \sum_{n=0}^{ \infty }(-1)^n \frac{x^{2n+1}}{(2n+1)!} = x – \frac{x^3}{6} + \frac{x^5}{120} – \cdots\)
将\(\frac{x}{2}\)带入上述泰勒展开式,即可看出\(sin(\frac{x}{2}) < \frac{x}{2}\)。不等式两边同时平方、并增加系数,不影响不等号方向:
\(2 \cdot sin(\frac{x}{2}) \cdot sin(\frac{x}{2}) < 2 \cdot \frac{x}{2} \cdot \frac{x}{2}\),从而完成了这一子问题的解答。